The ratio of gravitational mass to inertial mass is equal to:
12
2
1
None of these
The correct Answer is:C
To solve the question regarding the ratio of gravitational mass to inertial mass, we can follow these steps:
1. Understand the Definitions:
- Gravitational Mass (m_g): This is the mass that determines the strength of an object's interaction with the gravitational field. It is measured through the gravitational force acting on the object.
- Inertial Mass (m_i): This is the mass that determines an object's resistance to acceleration when a force is applied. It is measured by observing how much an object accelerates when a known force is applied.
2. Establish the Relationship:
- According to the principles of physics, particularly Newton's laws, gravitational mass and inertial mass are found to be equivalent. This means that the gravitational mass of an object is equal to its inertial mass.
3. Set Up the Ratio:
- The ratio of gravitational mass to inertial mass can be expressed mathematically as:
Ratio=mgmi
4. Substitute the Relationship:
- Since we have established that mg=mi, we can substitute this into the ratio:
Ratio=mgmg=1
5. Conclusion:
- Therefore, the ratio of gravitational mass to inertial mass is equal to 1.
Final Answer:
The ratio of gravitational mass to inertial mass is 1.
---
- Gravitational Mass (m_g): This is the mass that determines the strength of an object's interaction with the gravitational field. It is measured through the gravitational force acting on the object.
- Inertial Mass (m_i): This is the mass that determines an object's resistance to acceleration when a force is applied. It is measured by observing how much an object accelerates when a known force is applied.
- According to the principles of physics, particularly Newton's laws, gravitational mass and inertial mass are found to be equivalent. This means that the gravitational mass of an object is equal to its inertial mass.
- The ratio of gravitational mass to inertial mass can be expressed mathematically as:
Ratio=mgmi
- Since we have established that mg=mi, we can substitute this into the ratio:
Ratio=mgmg=1
- Therefore, the ratio of gravitational mass to inertial mass is equal to 1.
The ratio of gravitational mass to inertial mass is 1.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:SWOE
Explore 44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
Knowledge Check
The mass of moon 1% of mass of earth. The ratio of gravitational pull of earth on moon and that of moon on earth will be
A1:1B1:10C1:100D2:1If M is the mass of the earth and R its radius, then ratio of the gravitational acceleration and the gravitational constant is
AR2EMEBMER2ECMER2EDMERE
The ratio of the inertial mass to gravitational mass is equal to
View SolutionThe mass number of a nucleus is equal to
View SolutionThe mass number of a nucleus is equal to
View SolutionThe ratio of the mass of a certain volume of gas to the mass of an equal volume of hydrogen under the same conditions of temperature and pressure is known as_______
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
View SolutionWe know that when two equal masses are placed on a line then, gravitational force on a third mass is zero due to these two masses when the third is placed at the centre of line joining the two masses. But if third mass is placed anywhere else on the x-axis, the gravitational force acts on that mass due to these two masses. Consider a system shown in figure.
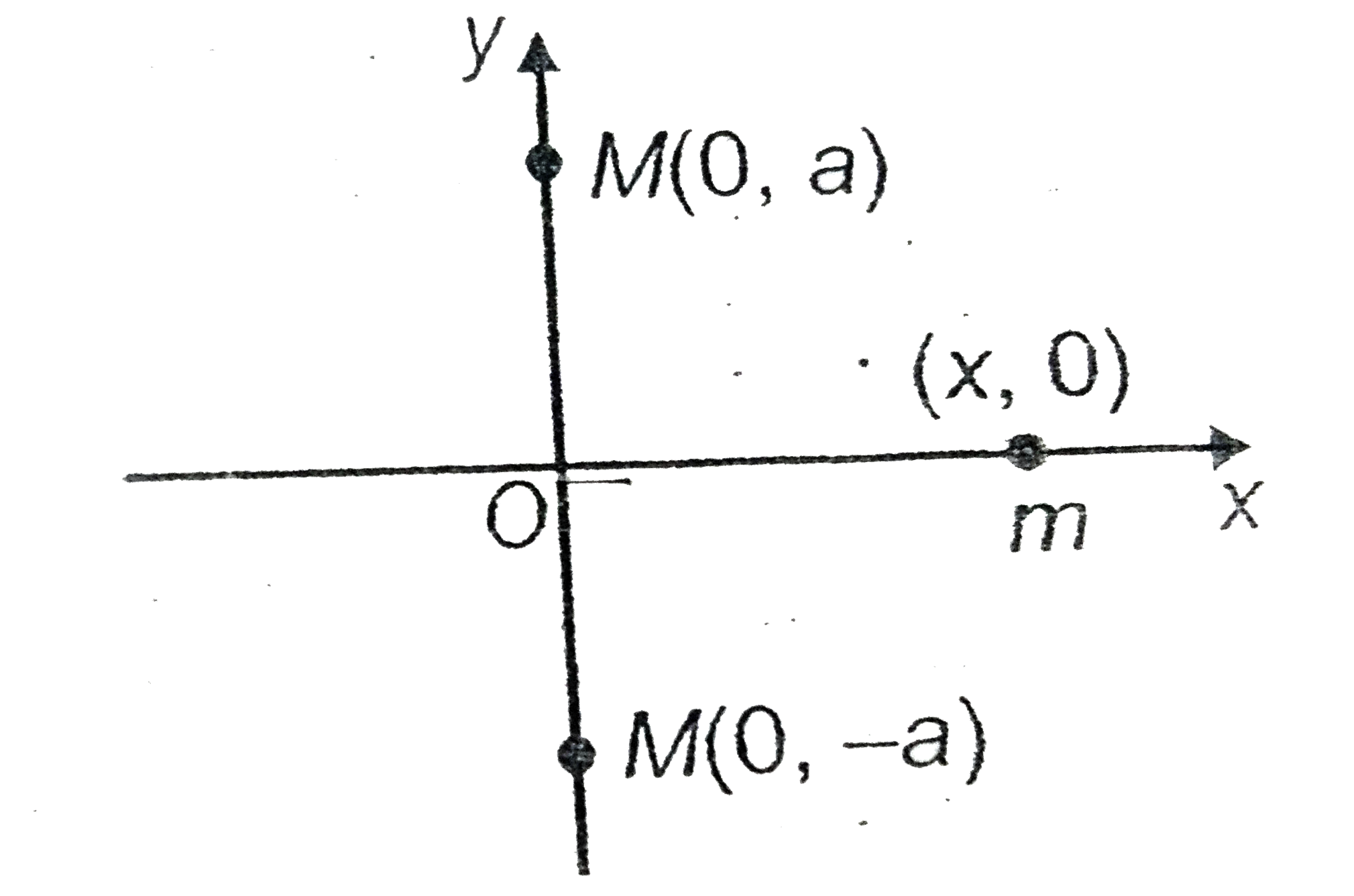
In this system two point masses of mass M each are placed at y-axis at a distance a from origin and these masses are fixed. If a third point mass of mass m is released at a distance x from origin on x-axis, then answer the following questions.
If a >> x, then which of the following statements is correct about the motion of mass m ?
View Solution

