The length of a nut cutter is 15cms. A force of 22.5kg is required to break a betal-nut without the aid of the cutter find where should the table nut be placed on the cutter so tht it can be cracket on application of 2.25 kg wt?
To solve the problem, we will use the principle of moments (torque) which states that for an object to be in equilibrium, the clockwise moments about a pivot point must equal the counterclockwise moments.
1. Identify the Given Data:
- Length of the nut cutter (lever arm) = 15 cm
- Force required to break the nut without the cutter = 22.5 kg
- Force applied with the cutter = 2.25 kg
2. Convert Forces to Newtons:
- Since weight is given in kg, we can convert it to Newtons using the relation F=m⋅g, where g≈9.8m/s2.
- Weight of the nut (without cutter):
F0=22.5kg×9.8m/s2=220.5N
- Weight applied with the cutter:
F1=2.25kg×9.8m/s2=22.05N
3. Set Up the Moment Equation:
- Let x be the distance from the fulcrum where the nut should be placed.
- The moment due to the nut (load) is:
Moment due to nut=F0⋅(15−x)
- The moment due to the applied force is:
Moment due to applied force=F1⋅x
4. Equate the Moments:
F0⋅(15−x)=F1⋅x
Substituting the values:
220.5⋅(15−x)=22.05⋅x
5. Expand and Rearrange the Equation:
220.5⋅15−220.5x=22.05x
3307.5−220.5x=22.05x
3307.5=220.5x+22.05x
3307.5=242.55x
6. Solve for x:
x=3307.5242.55≈13.63cm
7. Calculate the Distance from the Fulcrum:
- Since the total length of the cutter is 15 cm, the distance from the end of the cutter where the nut should be placed is:
15−x≈15−13.63≈1.37cm
Final Answer:
The nut should be placed approximately 1.37 cm from the end of the nut cutter.
- Length of the nut cutter (lever arm) = 15 cm
- Force required to break the nut without the cutter = 22.5 kg
- Force applied with the cutter = 2.25 kg
- Since weight is given in kg, we can convert it to Newtons using the relation F=m⋅g, where g≈9.8m/s2.
- Weight of the nut (without cutter):
F0=22.5kg×9.8m/s2=220.5N
- Weight applied with the cutter:
F1=2.25kg×9.8m/s2=22.05N
- Let x be the distance from the fulcrum where the nut should be placed.
- The moment due to the nut (load) is:
Moment due to nut=F0⋅(15−x)
- The moment due to the applied force is:
Moment due to applied force=F1⋅x
F0⋅(15−x)=F1⋅x
Substituting the values:
220.5⋅(15−x)=22.05⋅x
220.5⋅15−220.5x=22.05x
3307.5−220.5x=22.05x
3307.5=220.5x+22.05x
3307.5=242.55x
x=3307.5242.55≈13.63cm
- Since the total length of the cutter is 15 cm, the distance from the end of the cutter where the nut should be placed is:
15−x≈15−13.63≈1.37cm
The nut should be placed approximately 1.37 cm from the end of the nut cutter.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-I
Explore 52 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
A glass slab of thickness 2cm and refractive index 2 is placed in contact with a biconvex lens of focal length 20cm. The refractive index of the material of the lens 1.5 . The far side of the lens is silvered. Where should an object be placed in front of the slab so that it images on to itself?
View SolutionA plane mirror is placed 22.5 cm in front of the concave mirror of focal length 10 cm. Find where an object a can be placed between the two mirrors, so that the first image in both the mirrors coincides.
View Solution
Knowledge Check
A block A of mass 4 kg is placed on another block B of mass 5 kg and the block rests on a smooth horizontal table. For sliding the block A on B, a horizontal force of 12 N is required to be applied on it. The maximum horizontal force that can be applied on B so that both A and B move together and the acceleration produced by this force is
 A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
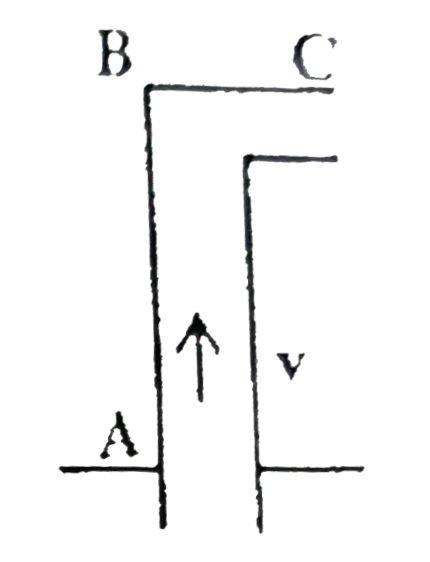
ABC is a light pipe lying in a vertical plane and of cross sectional area 1cm2 whose small part is in ground to fix the pipe. An ideal fluid of density 104kg/m3 is being flown through the pipe by means of external agency. Length of BC can be neglected. The minimum vertical upward force required to pull out the pipe from ground is F=9N. What should be maximum velocity (in m/s) of the fluid so that pipe can not be pulled out from ground ?
View SolutionA uniform horizontal rod of length 40 cm and mass 1.2 kg is supported by two identical wires as shown in figure. Where should a mass of 4.8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone ? Take g=10ms−2

View SolutionA block A of mass 4 kg is placed on another block B of mass 5 kg , and the block B rests on a smooth horizontal table . For sliding block A on B , a horizontal force of 12 N is required to be applied on A How much maximum force can be applied on B so that both A and B move togrther ? Also find out acceleration produced by this force .
View SolutionA block A of mass 4 kg is placed on another block B of mass 5 kg , and the block B rests on a smooth horizontal table . For sliding block A on B , a horizontal force of 12 N is required to be applied on A How much maximum force can be applied on B so that both A and B move togrther ? Also find out acceleration produced by this force .
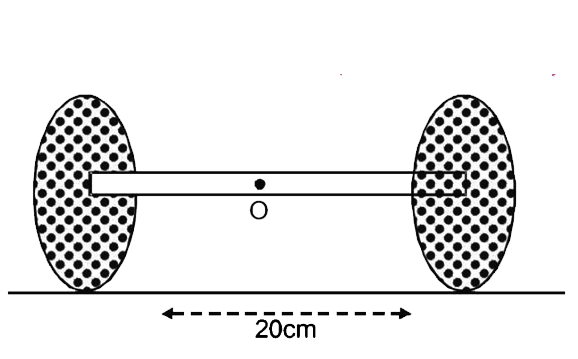
View SolutionTwo thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.
View SolutionA nut is opened by a wrench of length 10cm. IF the least force required is 5.0N, find the moment of force needed to turn the nut.
View SolutionA nut is opened by a wrench of length 20 cm. If the least force required is 2 N, find the moment of force needed to loosen the nut.
View Solution

