Question

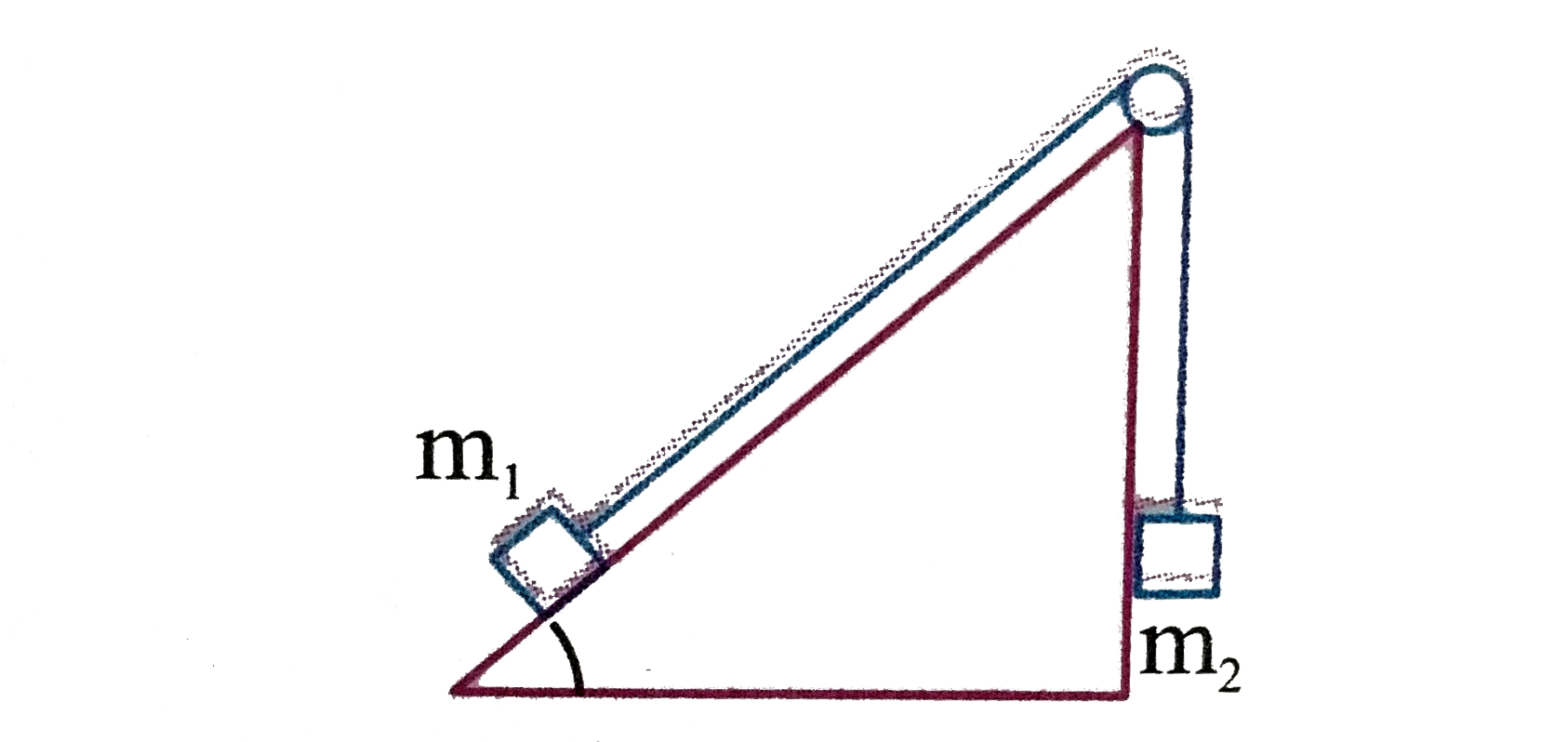
Two blocks of masses ${\displaystyle m_1=1kg\text{and}{m}_2=2kg}$ are connected by a string and side down a plane inclined at an angle ${\displaystyle \theta ={45}^{\circ }}$ with the horizontal. The coefficient of sliding friction between ${\displaystyle m_1}$ and plane is ${\displaystyle {\mu }_1=0.4,}$ and that between ${\displaystyle m_2}$ and plane is ${\displaystyle {\mu }_2=0.2.}$ Calculate the common acceleration of the two blocks and the tension in the string.

Explanation

As `mu_(2)ltmu_(1)`. Block `m_(2)` has greater acceleration than `m_(1)` if we separately consider the motion of blocks. But they are connected so they move together as a system with common acceleration.
So acceleration of the bloks: `a=((m_(1)+m_(2))g sin theta-mu_(1)m_(2)g cos theta-mu_(2)m_(2)g cos theta)/(m_(1)+m_(2))`
`=((1+2)(10)((1)/sqrt2)-0.4xx1xx10xx(1)/sqrt(2)-0.2xx2xx10xx(1)/sqrt(2))/(1+2)=(22)/(3sqrt(2))ms^(-2)~
For block `m_(2)`: `m_(2)g sin theta-mu_(2)m_(2)g cos theta-T=m_(2)arArrT=m_(2)g sin theta-mu_(2)gcos theta-m_(2)a`
`=2xx10xx(1)/sqrt(2)-0.2xx2xx10xx(1)/sqrt(2)-2xx(22)/(3sqrt(2))=(2)/(3sqrt(2))N`