The figure below depicts the paths of two colliding steel balls, A and B. Which of the arrows 1−4 best represents the impulse applied to ball A during the collision?
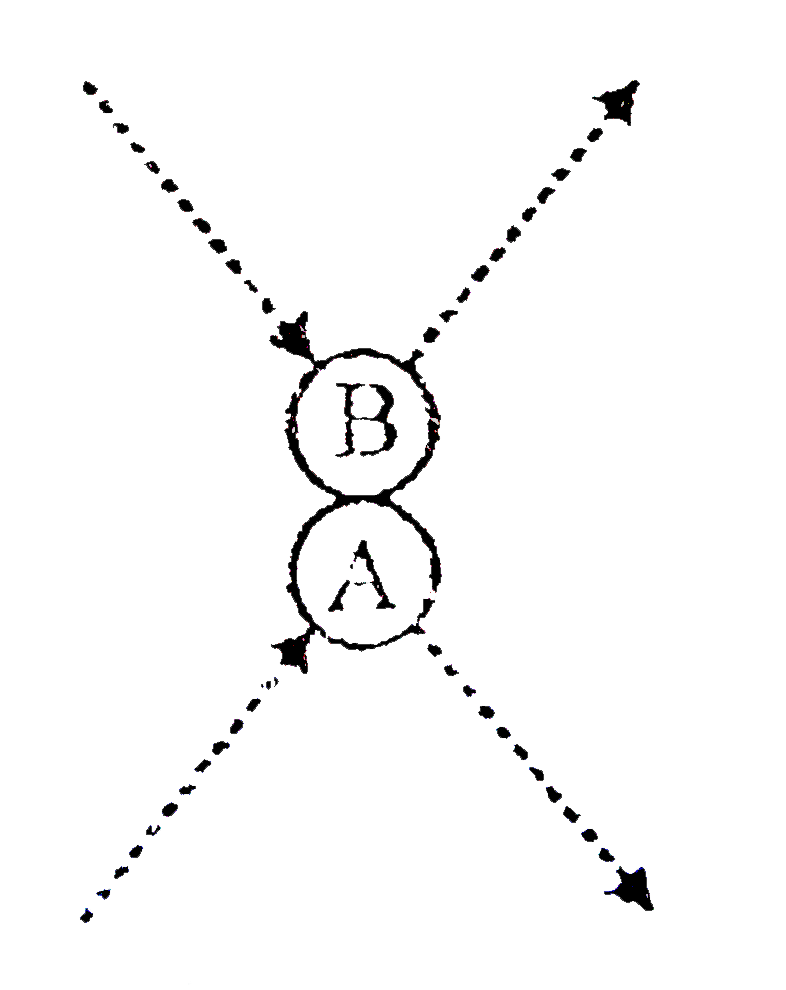

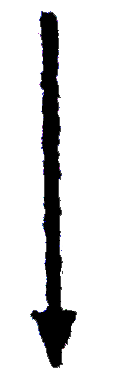


The correct Answer is:B
Ans.(2)
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
The figure below shows three identical balls A , B and C. Initially , the baiis B and C are at rest and the ball A while moving with a veiocity v, collides with ball B. if the collision is perfectiy elastic , then after the collision

View SolutionTwo smooth balls A and B, each of mass m and radius R, have their centers at (0, 0, R) and at (5R, -R, R) respectively, in a coordinate system as shown. Ball A, moving along positive x axis, collides with ball B. Just before the collision, speed of ball A is 4m/s and ball B is stationary. The collision between the ball is elastic.

Impulse of the force exerted by A and B during the collision, is equal to
View SolutionTwo smooth balls A and B, each of mass m and radius R, have their centre at (0,0,R) and (5R,-R,R) respectively, in a coordinate system as shown. Ball A, moving along positive x-axis, collides with ball B. Just before the collision, speed of ball A is 4m/s and ball B is stationary. The collision between the balls is elastic. Velocity of the ball A just after the collsion is
A. (ˆi+√3ˆj)m/s
B. (ˆi−√3ˆj)m/s
C. (2ˆi+√3ˆj)m/s
D. (2ˆi+2ˆj)m/s
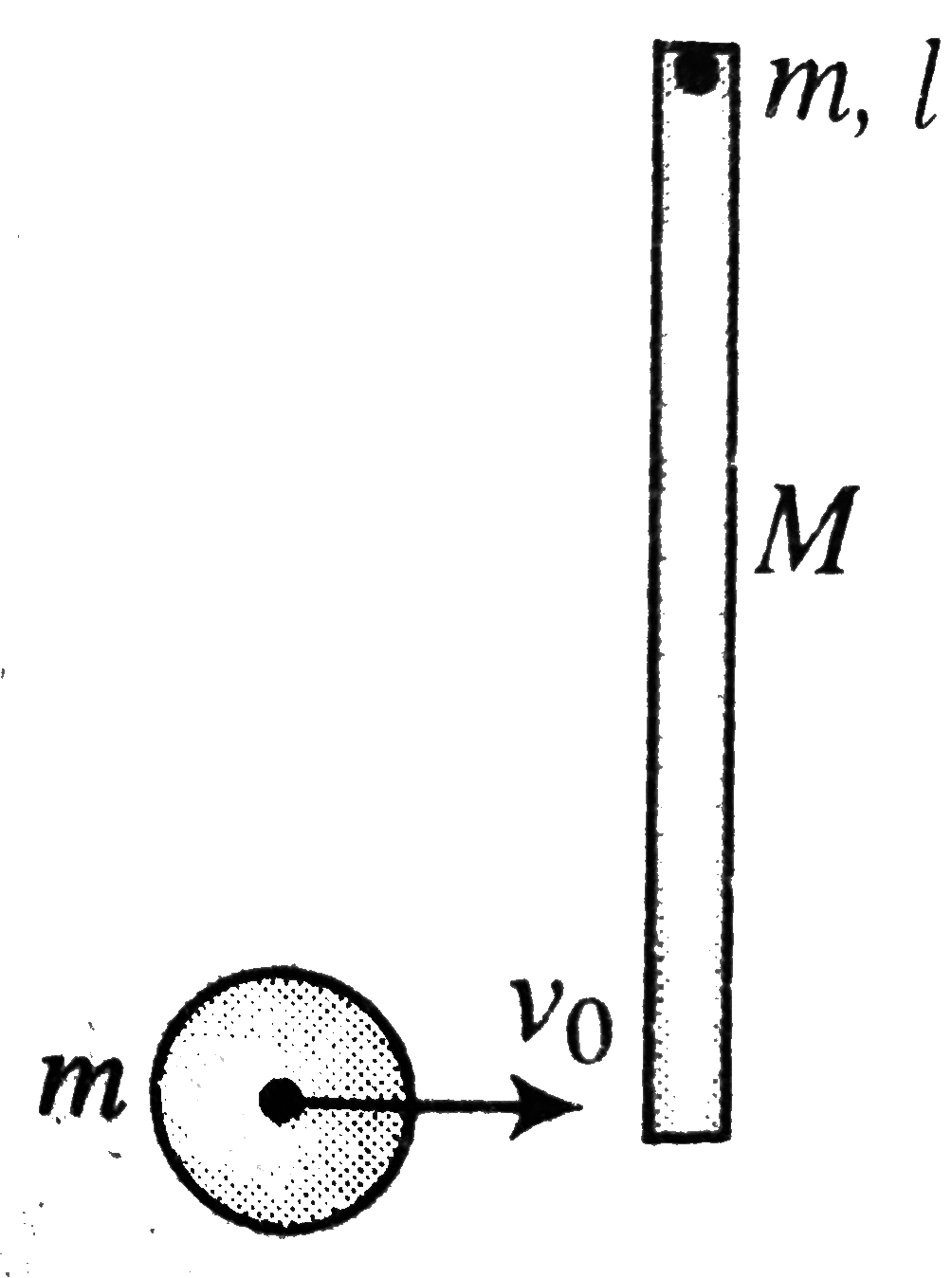
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA ball of mass m moving vertically down , collides with inclined surface of the wedge . After the collision , wedge starts moving in horizontal direction with velocity v0 . If all the surfaces are smooth then impulse applied by wedge on the ball during collision is given by

View SolutionTwo balls of same mass are dropped from the same height h, on to the floor. The first ball bounces to a height h/4, after the collision & the second ball to a height h/16. The impulse applied by the first & second ball on the floor are I1 and I2 respectively. Then :-
View SolutionTwo identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.

What is the impulse generated in the string during the first collision?
View SolutionA ball of mass m moving horizontally at a speed v collides with the bob of a simple pendulum at rest. The mass of the bob is also m. If the collision is perfectly elastic and both balls sticks, the height to which the two balls rise after the collision will be given by:
View SolutionSTATEMENT - 1 : Two identical balls B and C lie on a horizontal smooth straight groove so that they are touching. A third identical ball A moves at a speed v along the groove. And collides with B as shown in figure. If the collisions are perfectly elastic, then after the collision, balls A and B will come to rest and ball C moves with velocity v to the right.
because

STATEMENT - 2 : In an elastic collision, linear momentum and kinetic energy are both conserved.
View SolutionTwo identical balls A and B lie on a smooth horizontal surface, which gradually merges into a curve to a height 3.2m. Ball A is given a velocity of 10m/s, to collide head-on with ball B, which then takes up the curved path. What is the minimum coefficient of restitution, e, for the collision between A and B in order that ball B reaches the highest point C of the curve.

View Solution
