A disc of radius R=2m starts rotating wth constant angular acceleration α=(2rad)/s2. A block of mass m=2kg is kept at a distance R2 from the centre of disc. The coeffiecient of friction between disc and block is μs=0.4,μk=0.3. Acceleration of block when it just slips w.r.t. ground and w.r.t. disc are respectively−(g=10ms−2)
3ms−2,1ms−2
1ms−2,3ms−2
4ms−2,1ms−2
4ms−2,3ms−2
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the block and apply the concepts of friction and circular motion.
Step 1: Identify the given parameters
- Radius of the disc, R=2m
- Angular acceleration, α=2rad/s2
- Mass of the block, m=2kg
- Distance of the block from the center of the disc, r=R2=1m
- Coefficient of static friction, μs=0.4
- Coefficient of kinetic friction, μk=0.3
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the maximum static friction force
The maximum static friction force Fs that can act on the block is given by:
Fs=μs⋅N
where N is the normal force. The normal force on the block is equal to its weight since there are no vertical accelerations:
N=m⋅g=2kg⋅10m/s2=20N
Thus, the maximum static friction force is:
Fs=μs⋅N=0.4⋅20N=8N
Step 3: Calculate the required centripetal force
The block is at a distance r=1m from the center of the disc. The centripetal force Fc required to keep the block moving in a circle is given by:
Fc=m⋅ac
where ac is the centripetal acceleration, which can be expressed in terms of angular acceleration:
ac=r⋅α=1m⋅2rad/s2=2m/s2
Thus, the required centripetal force is:
Fc=m⋅ac=2kg⋅2m/s2=4N
Step 4: Determine if the block slips
The block will slip when the required centripetal force exceeds the maximum static friction force:
Fc>Fs⟹4N>8N
Since this is not true, the block will not slip due to static friction until the angular velocity increases.
Step 5: Calculate the acceleration of the block when it just slips
When the block starts to slip, the kinetic friction force Fk will act on it:
Fk=μk⋅N=0.3⋅20N=6N
The net force acting on the block when it slips is:
Fnet=Fk−Fc=6N−4N=2N
Using Newton's second law, we can find the acceleration a of the block:
Fnet=m⋅a⟹2N=2kg⋅a⟹a=1m/s2
Step 6: Calculate the acceleration of the block with respect to the ground
The acceleration of the block with respect to the ground when it just slips is the sum of the acceleration due to kinetic friction and the centripetal acceleration:
aground=a+ac=1m/s2+2m/s2=3m/s2
Final Answers
- Acceleration of the block when it just slips with respect to the ground: 3m/s2
- Acceleration of the block when it just slips with respect to the disc: 1m/s2
- Radius of the disc, R=2m
- Angular acceleration, α=2rad/s2
- Mass of the block, m=2kg
- Distance of the block from the center of the disc, r=R2=1m
- Coefficient of static friction, μs=0.4
- Coefficient of kinetic friction, μk=0.3
- Acceleration due to gravity, g=10m/s2
The maximum static friction force Fs that can act on the block is given by:
Fs=μs⋅N
where N is the normal force. The normal force on the block is equal to its weight since there are no vertical accelerations:
N=m⋅g=2kg⋅10m/s2=20N
Thus, the maximum static friction force is:
Fs=μs⋅N=0.4⋅20N=8N
The block is at a distance r=1m from the center of the disc. The centripetal force Fc required to keep the block moving in a circle is given by:
Fc=m⋅ac
where ac is the centripetal acceleration, which can be expressed in terms of angular acceleration:
ac=r⋅α=1m⋅2rad/s2=2m/s2
Thus, the required centripetal force is:
Fc=m⋅ac=2kg⋅2m/s2=4N
The block will slip when the required centripetal force exceeds the maximum static friction force:
Fc>Fs⟹4N>8N
Since this is not true, the block will not slip due to static friction until the angular velocity increases.
When the block starts to slip, the kinetic friction force Fk will act on it:
Fk=μk⋅N=0.3⋅20N=6N
The net force acting on the block when it slips is:
Fnet=Fk−Fc=6N−4N=2N
Using Newton's second law, we can find the acceleration a of the block:
Fnet=m⋅a⟹2N=2kg⋅a⟹a=1m/s2
The acceleration of the block with respect to the ground when it just slips is the sum of the acceleration due to kinetic friction and the centripetal acceleration:
aground=a+ac=1m/s2+2m/s2=3m/s2
- Acceleration of the block when it just slips with respect to the ground: 3m/s2
- Acceleration of the block when it just slips with respect to the disc: 1m/s2
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A disc of radius 5 m is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
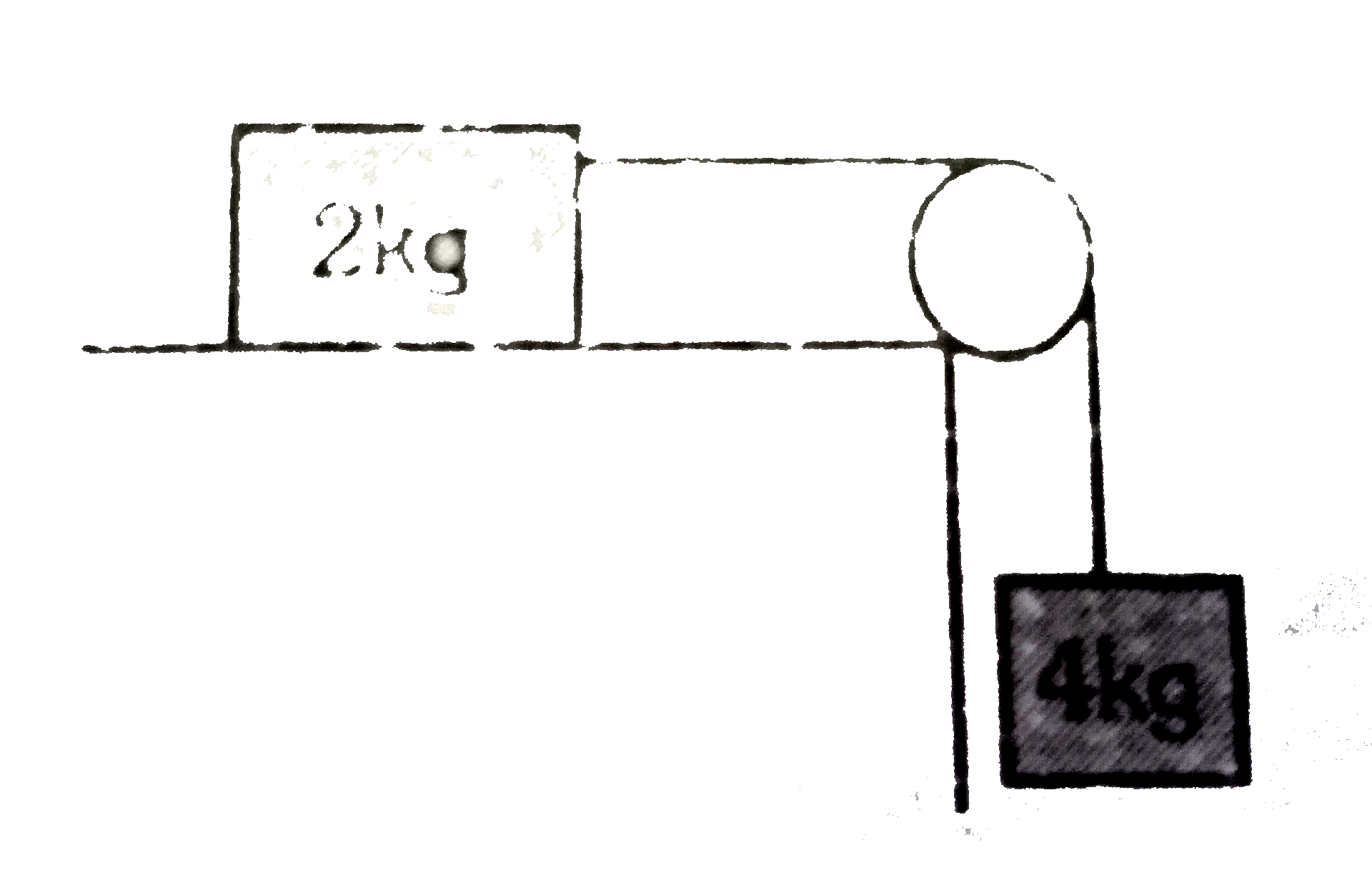
View SolutionA disc starts rotating with a constant angular acceleration of 1rad/s2 about a fixed vertical axis perpendicular to its plane and passing through its centre. A coin of mass 10gm is placed on the disc at a distance of 10cm from the axis. The coefficent of friction between the disc and the coin is 0.2. The value of the frictional force on the coin at t=1s will be
View SolutionAt time t = 0 , a horizontal disc starts rotating with angular acceleration 1 red s about an axis perpendicular to its plane and passing through its centre. A small block is lying on this disc at a distance 0.5 m from the centre. Coefficient of friction between the surface of block and disc is 0.255. The block will start slipping on the disc at time t . Which is approximately equal to
View SolutionA disc of mass 2 kg and radius 0.2 m is rotating with angular velocity 30rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc ?
View SolutionIf block A is moving with an acceleration of 5ms−2, the acceleration of B w.r.t. ground is

View SolutionA uniiform disc of radius r spins with angular velocity ω and angular acceleration α. If the centre of mass of the disc has linear acceleration a, find the magnitude and direction of aceeleration of the point 1,2, and 3.
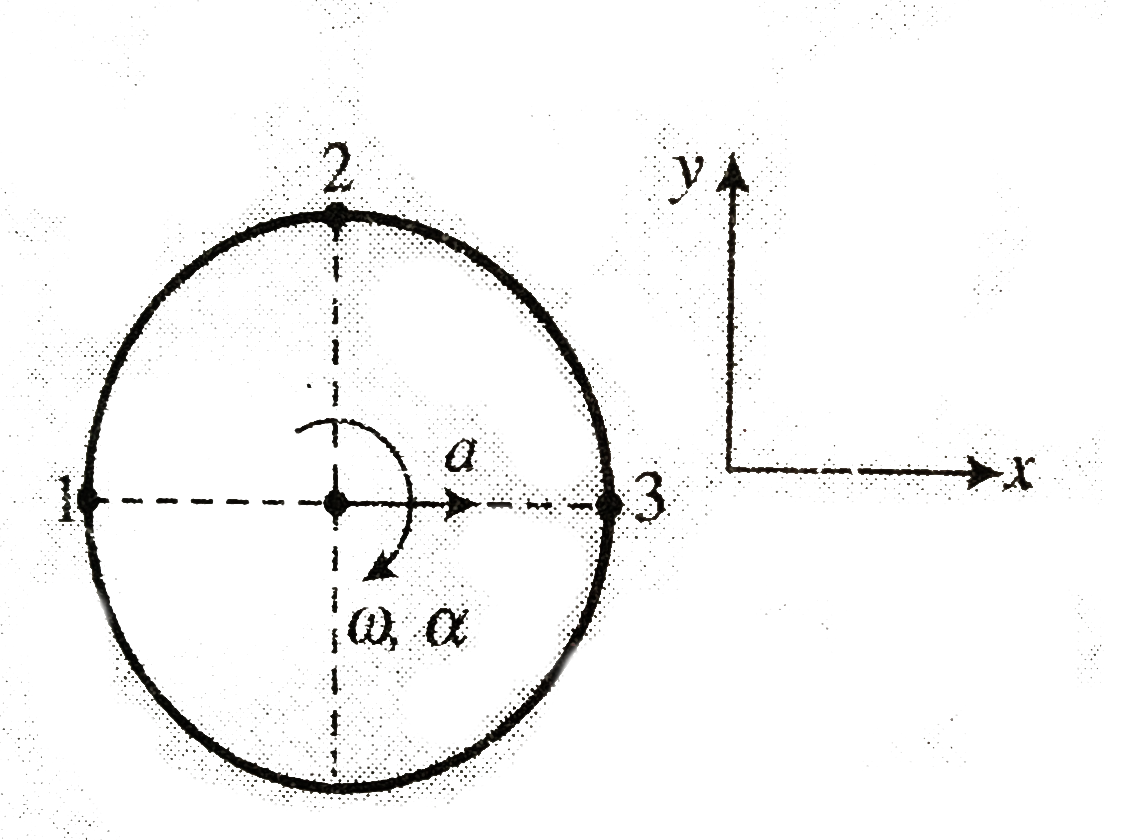
View SolutionA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View Solution
