A uniform wire frame ABC is in the shape of an equilateral triangle in xy−plane with centroid at the orgin. Then:−

If AB is removed, the centre of mass of the remaining figure is in fourth quadrant.
If BC is removed, the centre of mass of the remaining figure is on the positive Y−axis.
If AC is removed, the centre of mass of the remaining figure is in third quadrant.
All of above.
The correct Answer is:D

When BC is removed, frame is symmetric about Y−axis⇒COM shifts towards A i.e. on Y−axis only.
When AB is removed frame is symmetric about OY'⇒ shifts towards C When AC is removed, frame is symmetric about OY⇒ COM shifts towards B
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
One vertex of the equilateral triangle with centroid at the origin and one side as x+y−2=0 is :
View SolutionA wire frame in the shape of an equilateral triangle is hinged at one vertex so that it can swing freely in a vertical plane, with the plane of the Δ always remaining vertical. The side of the frame is 1/√3m. The time period in seconds of small oscillations of the frame will be-
View SolutionA current of 2A is flowing in the sides of an equilateral triangle of side 9 cm. The magnetic field at the centroid of the triangle is
View SolutionA piece of land is in the shape of an equilateral triangle. Its boundary has to be fenced with barbed wire. What is the length of the barbed wire required?
View SolutionABC is a plane lamina of the shape of an equilateral triangle. D , E are mid points of AB,AC and G is the centroid of the lamina . Moment of inertia of the lamina about an axis passing through G and perpendicular to the plane ABC is I0 If part ADE is removed, the moment of inertia of a remaining part about the same axis is NI016 where N is an integer . Value of N is
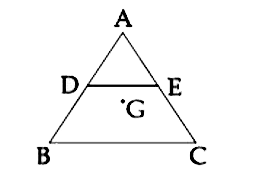
View SolutionFind the coordinates of one vertex of an equilateral triangle with centroid at the origin and the opposite side x+y−2=0.
View SolutionA current of 1⋅0A flowing in the sides of an equilateral triangle of side 4⋅5×10−2m. Find the magnetic fied at the centroid of the triangle.
View SolutionA wire of length 20m is to be cut into two pieces. One of the places will be bent into shape of a square and the other shape of an equilateral triangle. Where the wire should be cut so that the sum of the areas of the square and triangle is minimum?
View SolutionA piece of wire is bent in the shape of an equilateral triangle of each side 6.6 cm. It is re-bent to form a circular ring. What is the diameter of the ring?
View SolutionThe wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.

View Solution
