A ball of mass impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impringes be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
The correct Answer is:C
To solve the problem step by step, we will follow the principles of conservation of momentum and the definition of the coefficient of restitution.
Step 1: Understand the scenario
We have two balls:
- Ball A (mass = 2m) is moving with velocity v.
- Ball B (mass = m) is at rest (velocity = 0).
Step 2: Apply the conservation of momentum
According to the law of conservation of momentum, the total momentum before the collision must equal the total momentum after the collision.
Before the collision:
- Momentum of Ball A = 2m⋅v
- Momentum of Ball B = m⋅0=0
Total initial momentum = 2m⋅v+0=2mv
After the collision:
Let the velocity of Ball A after the collision be v′ and the velocity of Ball B after the collision be v (as given in the problem).
- Momentum of Ball A after collision = 2m⋅v′
- Momentum of Ball B after collision = m⋅v
Total final momentum = 2m⋅v′+m⋅v
Setting the initial momentum equal to the final momentum:
2mv=2mv′+mv
Step 3: Simplify the equation
We can simplify the equation by dividing everything by m:
2v=2v′+v
Rearranging gives:
2v−v=2v′
v=2v′
Step 4: Solve for v′
From the equation v=2v′, we can express v′:
v′=v2
Step 5: Calculate the coefficient of restitution
The coefficient of restitution e is defined as the ratio of the relative velocity of separation to the relative velocity of approach.
Relative velocity of approach:
Before the collision, the relative velocity of approach is simply the velocity of Ball A since Ball B is at rest:
Relative velocity of approach=v−0=v
Relative velocity of separation:
After the collision, the relative velocity of separation is:
Relative velocity of separation=v′−0=v′
Substituting v′=v2:
Relative velocity of separation=v2
Step 6: Calculate the coefficient of restitution
Now, substituting these values into the formula for the coefficient of restitution:
e=Relative velocity of separationRelative velocity of approach=v2v
Simplifying this gives:
e=12
Conclusion
The coefficient of restitution is 12.
We have two balls:
- Ball A (mass = 2m) is moving with velocity v.
- Ball B (mass = m) is at rest (velocity = 0).
According to the law of conservation of momentum, the total momentum before the collision must equal the total momentum after the collision.
- Momentum of Ball A = 2m⋅v
- Momentum of Ball B = m⋅0=0
Let the velocity of Ball A after the collision be v′ and the velocity of Ball B after the collision be v (as given in the problem).
- Momentum of Ball B after collision = m⋅v
We can simplify the equation by dividing everything by m:
v=2v′
From the equation v=2v′, we can express v′:
The coefficient of restitution e is defined as the ratio of the relative velocity of separation to the relative velocity of approach.
Before the collision, the relative velocity of approach is simply the velocity of Ball A since Ball B is at rest:
After the collision, the relative velocity of separation is:
Now, substituting these values into the formula for the coefficient of restitution:
The coefficient of restitution is 12.
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-II
Explore 43 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-III
Explore 42 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V B
Explore 19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
A ball of mass m is thrown upward with a velocity υ. If air exerts an average resisting force F, the velocity with which the ball returns to the thrower is
View SolutionA ball collides impinges directly on a similar ball at rest. The first ball is brought to rest after the impact. If half of the kinetic energy is lost by impact, the value of coefficient of restitution (e) is
View SolutionA ball collides impinges directly on a similar ball at rest. The first ball is brought to rest after the impact. If half of the kinetic energy is lost by impact, the value of coefficient of restitution (e) is
View SolutionA ball of mass 4kg moving with a velocity of 12m/s impinges directly on another ball of mass 8kg moving with velocity of 4m/s in the same direction. Find their velocities after impact and calculate the loss of KE due to impact if e=0.5.
View SolutionA sphere of mass m, impinges obliquely on a sphere, of mass M, which is at rest. Show that, if m=eM, the directions of motion of the sphere after impact are at right angles.
View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 34th of the original. Find the coefficient of restitution.


View SolutionA ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?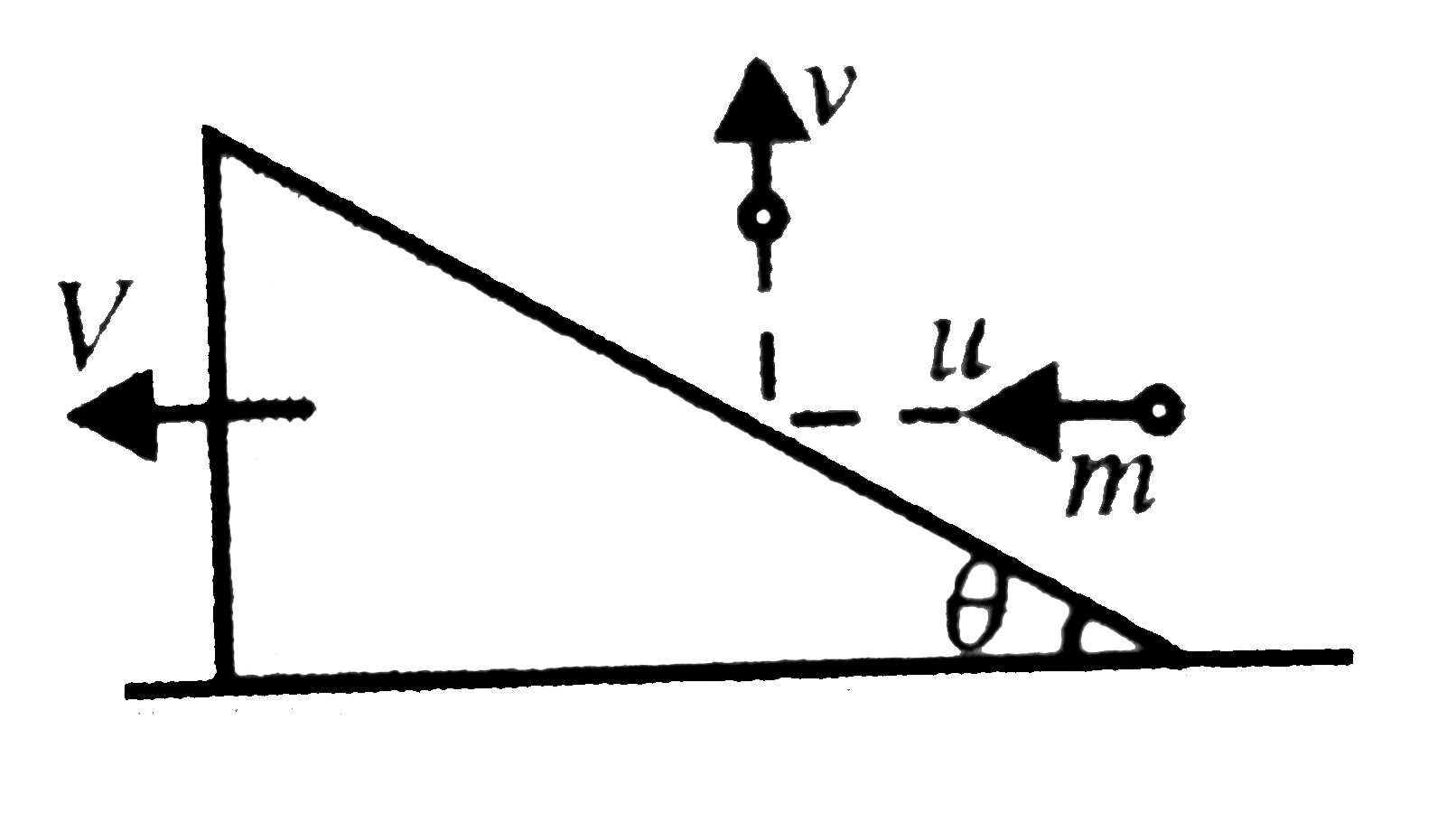
View SolutionA ball of mass m, travelling with velocity 2ˆi+3ˆj receives an impulse −3mˆi. What is the velocity of the ball immediately afterwards?
View SolutionIf the collision of a ball of mass m is inelastic, then the relation between theta and alpha is (where theta is the coefficient of restitution)
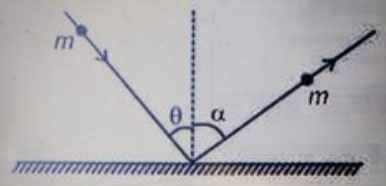
View SolutionA ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View Solution