A ball of mass m, travelling with velocity 2ˆi+3ˆj receives an impulse −3mˆi. What is the velocity of the ball immediately afterwards?
The correct Answer is:A, C
To solve the problem, we need to find the velocity of a ball after it receives an impulse. Let's break down the solution step by step.
1. Identify Given Values:
- Initial velocity of the ball, →vi=2^i+3^j
- Impulse received, →J=−3m^i
- Mass of the ball, m
2. Understand the Concept of Impulse:
- Impulse is defined as the change in momentum. Mathematically, it can be expressed as:
→J=Δ→p=m→vf−m→vi
- Here, →vf is the final velocity we want to find.
3. Set Up the Equation:
- Rearranging the impulse-momentum equation gives:
→J=m→vf−m→vi
- This can be rewritten as:
→J+m→vi=m→vf
4. Substituting the Values:
- Substitute the known values into the equation:
−3m^i+m(2^i+3^j)=m→vf
5. Simplifying the Equation:
- Distributing m in the equation:
−3m^i+2m^i+3m^j=m→vf
- Combine the terms:
(−3m+2m)^i+3m^j=m→vf
- This simplifies to:
−m^i+3m^j=m→vf
6. Dividing by Mass:
- Since m is non-zero, we can divide through by m:
→vf=−^i+3^j
7. Final Result:
- Therefore, the final velocity of the ball immediately after receiving the impulse is:
→vf=−^i+3^j
Final Answer:
The velocity of the ball immediately afterwards is −^i+3^j.
---
- Initial velocity of the ball, →vi=2^i+3^j
- Impulse received, →J=−3m^i
- Mass of the ball, m
- Impulse is defined as the change in momentum. Mathematically, it can be expressed as:
→J=Δ→p=m→vf−m→vi
- Here, →vf is the final velocity we want to find.
- Rearranging the impulse-momentum equation gives:
→J=m→vf−m→vi
- This can be rewritten as:
→J+m→vi=m→vf
- Substitute the known values into the equation:
−3m^i+m(2^i+3^j)=m→vf
- Distributing m in the equation:
−3m^i+2m^i+3m^j=m→vf
- Combine the terms:
(−3m+2m)^i+3m^j=m→vf
- This simplifies to:
−m^i+3m^j=m→vf
- Since m is non-zero, we can divide through by m:
→vf=−^i+3^j
- Therefore, the final velocity of the ball immediately after receiving the impulse is:
→vf=−^i+3^j
The velocity of the ball immediately afterwards is −^i+3^j.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.6
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.4
4 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A ball of mass 1 kg moving with velocity →v=3ˆi+4ˆj collides with a wall and after collision velocity of the ball is −2ˆi+6ˆj . Which of the following unit vectors is perpendicular to wall?
View SolutionA cricket ball of mass 200 gm moving with velocity 15 m/s is brought to rest by a player in 0.05 sec. What is the impulse of the ball and average force exerted by player ?
View SolutionA ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impringes be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View SolutionA ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, travelling with a velocity Vm/s in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The velocity V of the bullet is

View SolutionA mud ball at rest explodes into three fragmennts of masses in the ragio 1:2:1. the two equal masses move with velocities 2ˆi+5ˆj−6ˆk and −4ˆi+3ˆj+2ˆk. Find the velocity of the find mass.

View SolutionA ball of mass '2m' moving with velocity uˆi collides with another ball of mass 'm' moving with velocity −2uˆi. After the collision, mass 2m moves with velocity u2(ˆi−ˆj). Then the change in kinetic energy of the system ( both balls ) is
View SolutionA ball of mass m is thrown upward with a velocity υ. If air exerts an average resisting force F, the velocity with which the ball returns to the thrower is
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA body of mass 3 kg moving with a velocity (2ˆi+3ˆj+3ˆk) m/s collides with another body of mass 4 kg moving with a velocity (3ˆi+2ˆj−3ˆk) m/s. The two bodies stick together after collision. The velocity of the composite body is
View SolutionA ball of mass m moving with velocity v0 collides a wall as shown in figure. After impact it rebounds with a velocity 34v0. The impulse acting on ball during impact is
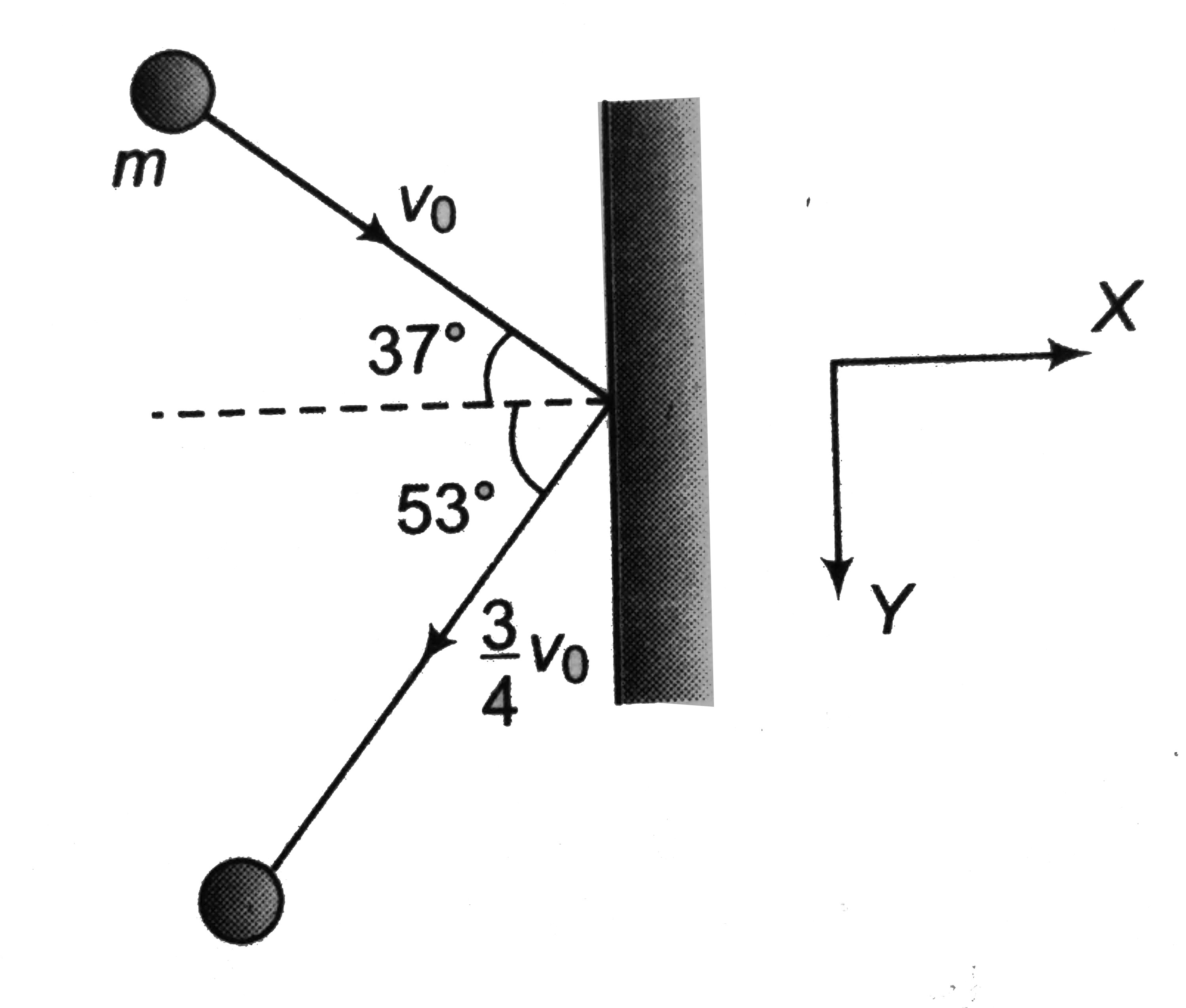
View Solution
