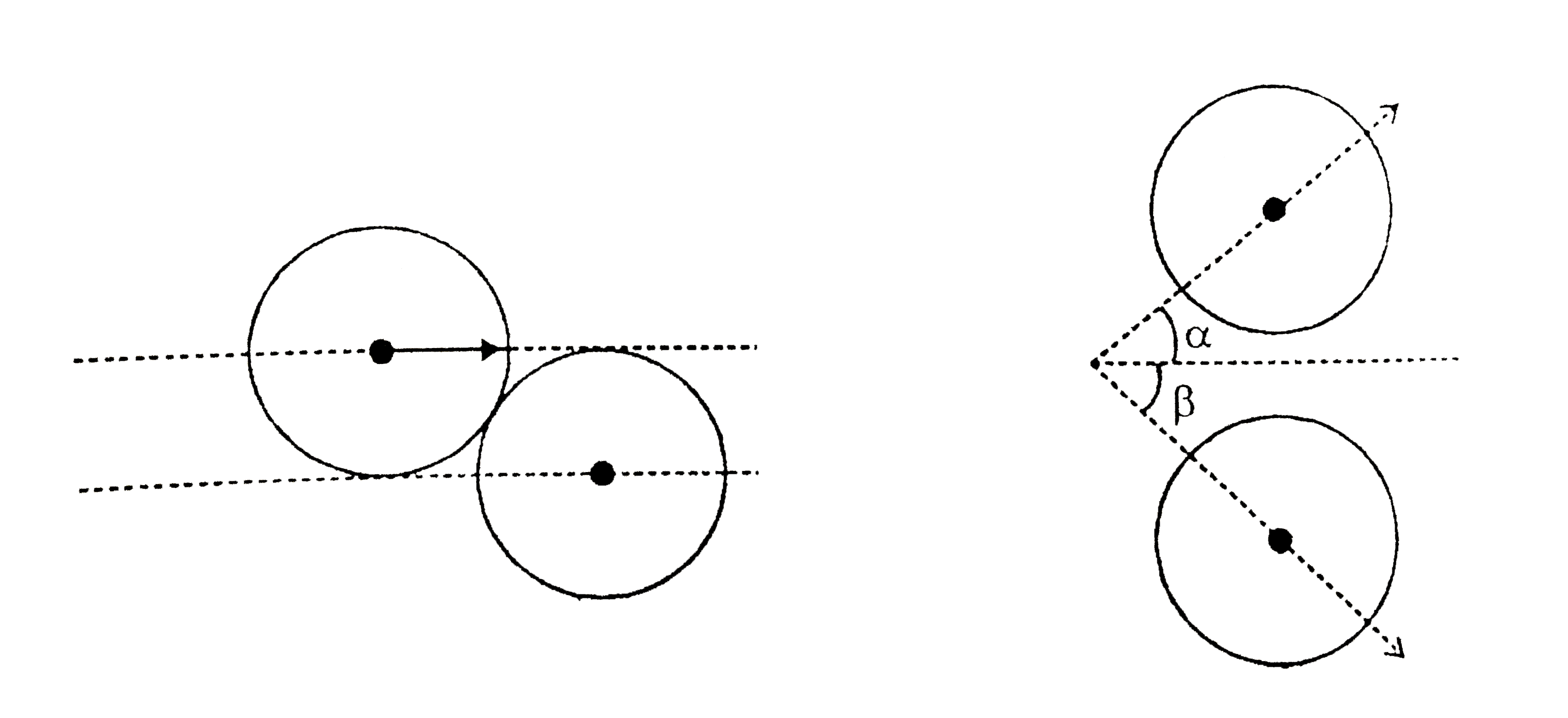
A moving 2kg ball with a speed of 2ms−1 hits obliquely a stationary identical ball inelastically as shown. If the first ball move away with angle α=30∘ to the original path, find the total kinetic energy lost after the collision
4/3J
5/4J
6/5J
7/6J
The correct Answer is:A

Tangential component remain same
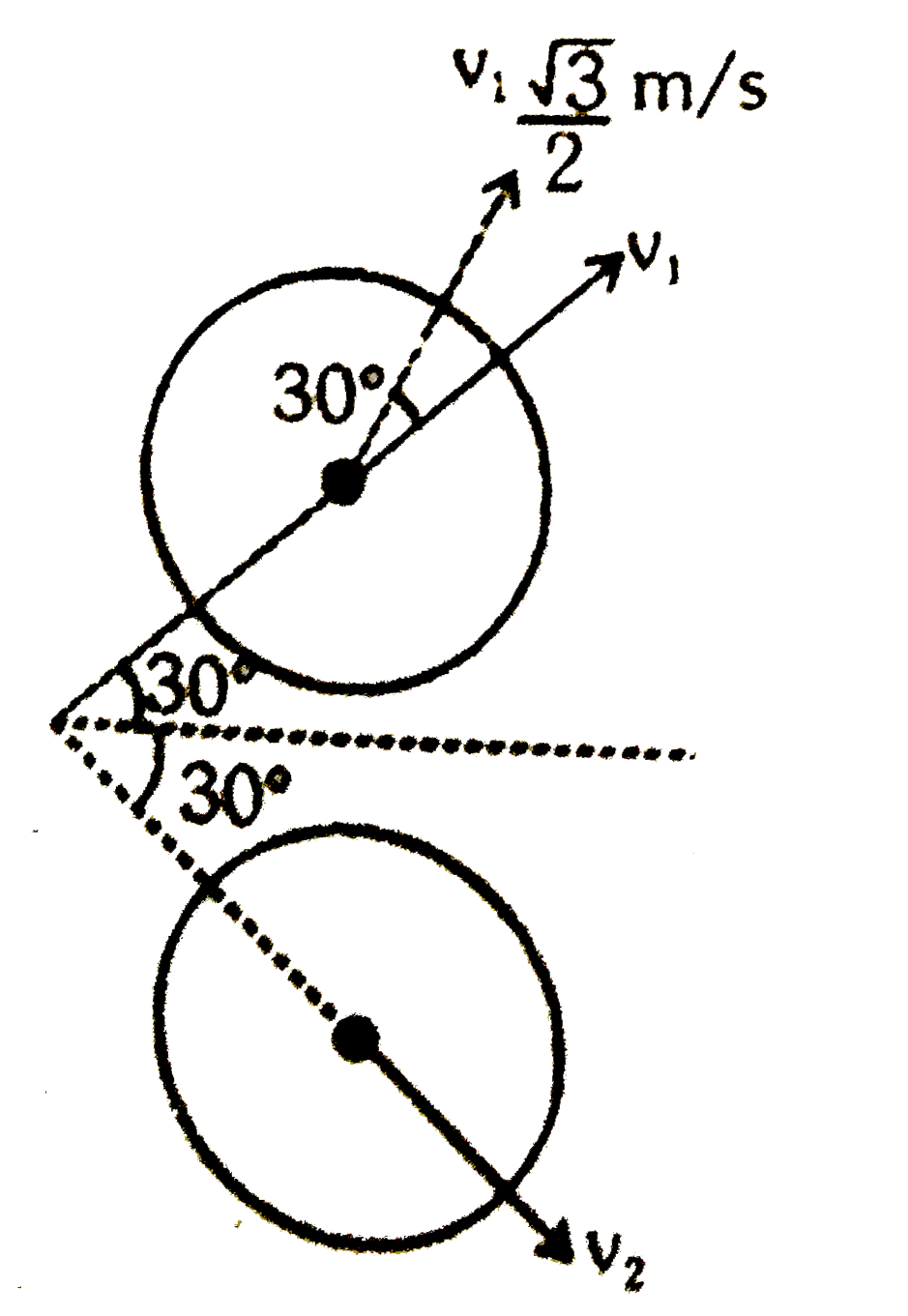
1=√3v12⇒v1=2√3
Momentum is conserved along normal
2√3=2×v12+2×v2⇒√3=1√3+v2
v2=2√3
ΔKE=12×2×4−⎛⎝12×2×(2√3)2+12×2×(2√3)2⎞⎠
=43J
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
42 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View SolutionA ball of mass m collides with a stationary identical ball a speed v0. Find the impulse of the colliding balls (e=1/2).
View Solution
Knowledge Check
A ball , moving with a speed of 10√3m/s , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of 30∘with the original line of motion. The speeds of two balla after the collision are , respectively.
A3ms−1,3ms−1B3√3ms−1,3√3ms−1C3√3ms−1,3ms−1D3ms−1,3√3ms−1
A ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionA smooth ball 'A' moving with velocity 'V' collides with another smooth identical ball at rest. After collision both the balls move with same speed with angle between their velocities 60∘. No external force acts on the system of balls.
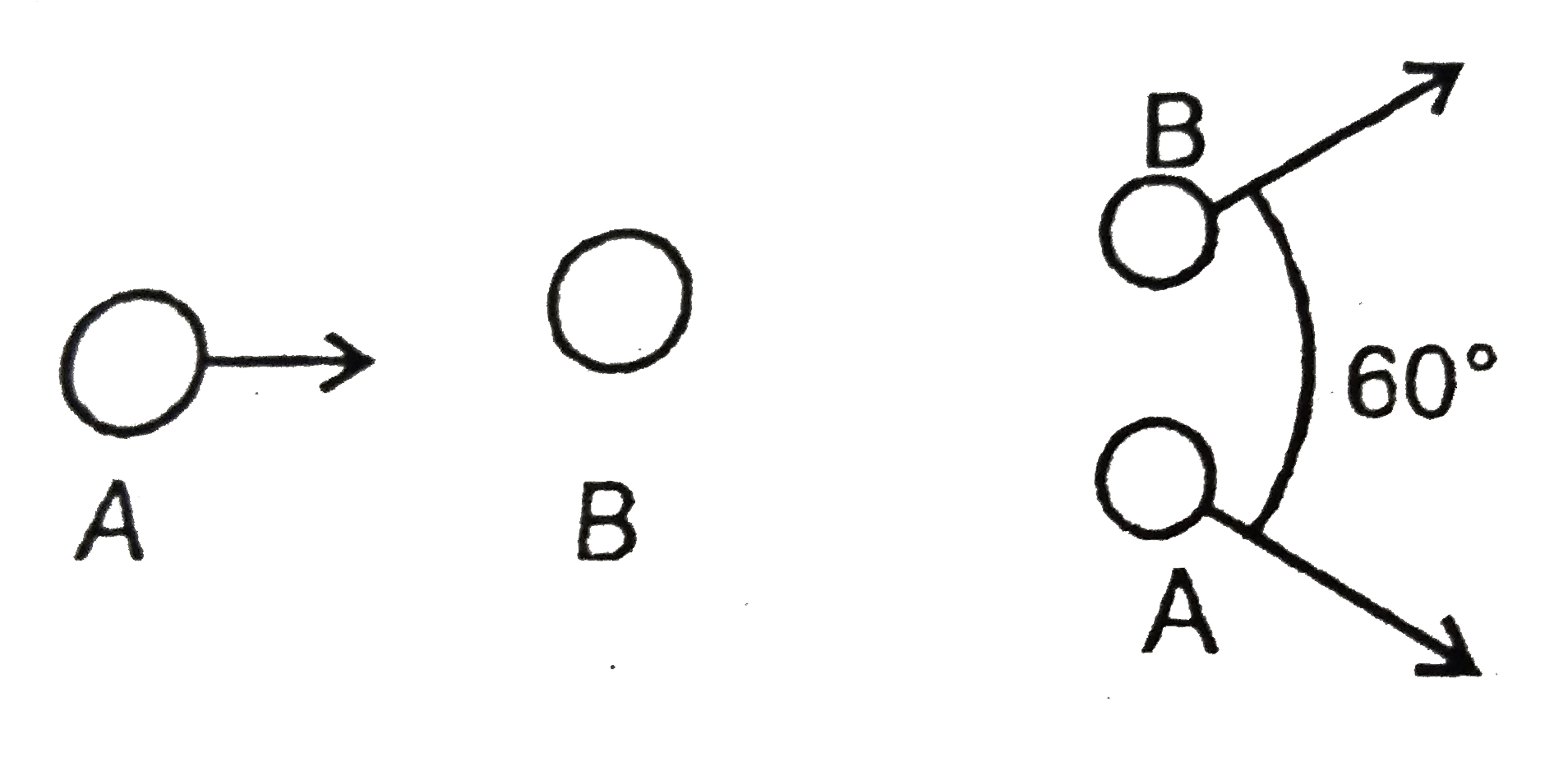
If the kinetic energy lost is fully converted to heat then heat produced is
View SolutionA smooth ball 'A' moving with velocity 'V' collides with another smooth identical ball at rest. After collision both the balls move with same speed with angle between their velocities 60∘. No external force acts on the system of balls.

The speed of each ball after the collision is
View SolutionA spherical ball of mass 1kg moving with a uniform speed of 1m/s collides symmetrically with two identical spherical balls of mass 1kg each at rest touching each other. If the two balls move with 0.5m/s in two directions at the same angle of 60∘ with the direction of the first ball, the loss of kinetic energy on account of the collision is :-
View SolutionAn iron ball A collides with another stationary iron ball B If the ratio of radii of the balls is n = 2, find the ratio of their speeds just after the collision (e = 0.5)

View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 34th of the original. Find the coefficient of restitution.


View SolutionA ball A moving with a velocity 5 m/s collides elastically with another identical ball at rest such that the velocity of A makes an angle of 30∘ with the line joining the centres of the balls. Then consider following statements :
(A) Balls A an B move at right angles after collision
(B) kinetic energy is conserved
(C) speed of A after collision is (5/2) m/s
(D) speed of B after collision is (5√3/2) m/s
Select correct alternative :-
View Solution
