Question

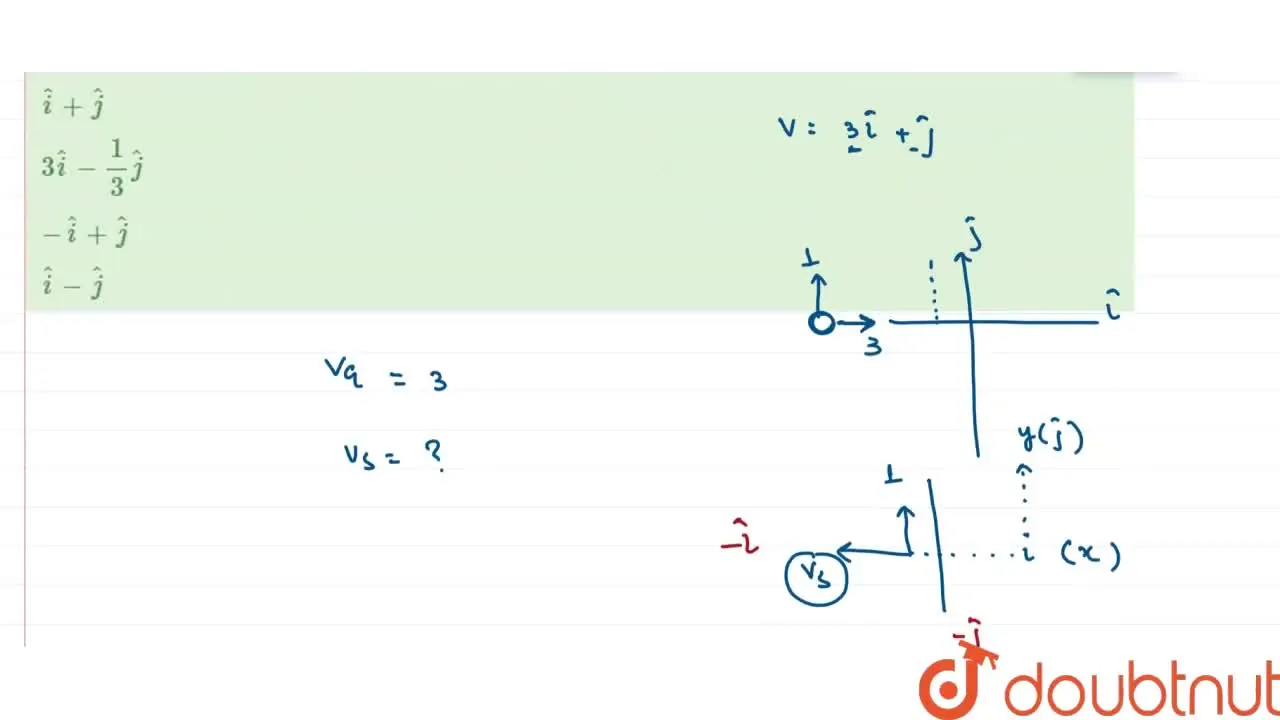
A smooth sphere is moving on a horizontal surface with velocity vector ${\displaystyle 3\hat{i}+\hat{j}}$ immediately before it hits a vertical wall. The wall is parallel to the vector ${\displaystyle \hat{j}}$ and the coefficient of restitution between the wall and sphere is ${\displaystyle \frac{1}{3}}$. The velocity vector of the sphere after it hits the wall is :-

Options

A. `hat(i) + hat(j)`
B. `3hat(i) - (1)/(3) hat(j)`
C. `-hat(i) + hat(j)`
D. `hat(i) - hat(j)`

Answer

C

Explanation

To solve the problem, we need to analyze the motion of the sphere before and after it collides with the wall. Here’s a step-by-step solution:

Step 1: Identify the initial velocity vector
The initial velocity vector of the sphere before it hits the wall is given as:
\( \vec{v_i} = 3\hat{i} + 1\hat{j} \)
This means the sphere is moving with a velocity of 3 m/s in the x-direction (i-direction) and 1 m/s in the y-direction (j-direction).

Step 2: Understand the wall's orientation
The wall is vertical and parallel to the j-direction. This means that the collision will affect only the x-component of the velocity, while the y-component will remain unchanged.

Step 3: Use the coefficient of restitution
The coefficient of restitution \( e \) is given as \( \frac{1}{3} \). The coefficient of restitution relates the velocities before and after the collision:
\( e = \frac{\text{Rate of separation}}{\text{Rate of approach}} \)

Step 4: Define rate of approach and rate of separation
- Rate of approach (\( v_a \)): This is the velocity component of the sphere towards the wall, which is the x-component of the initial velocity:
\( v_a = 3 \text{ m/s} \)

- Rate of separation (\( v_s \)): This is the x-component of the velocity after the collision, which we need to find.

Step 5: Apply the coefficient of restitution formula
Using the formula for the coefficient of restitution:
\( e = \frac{v_s}{v_a} \)
Substituting the known values:
\( \frac{1}{3} = \frac{v_s}{3} \)

Step 6: Solve for the rate of separation
To find \( v_s \), we can rearrange the equation:
\( v_s = e \cdot v_a = \frac{1}{3} \cdot 3 = 1 \text{ m/s} \)
Since the sphere is bouncing back, the direction of \( v_s \) will be negative in the i-direction:
\( v_s = -1 \hat{i} \text{ m/s} \)

Step 7: Determine the final velocity vector
After the collision:
- The x-component of the velocity is \( -1 \hat{i} \).
- The y-component of the velocity remains unchanged at \( 1 \hat{j} \).

Thus, the final velocity vector of the sphere after it hits the wall is:
\( \vec{v_f} = -1\hat{i} + 1\hat{j} \)

Final Answer
The velocity vector of the sphere after it hits the wall is:
\( \vec{v_f} = -\hat{i} + \hat{j} \)

---