A ball of mass 1kg is projected horizontally as shown in figure. Assume that collision between the ball and ground is totally inelastic. The kinetic energy of ball in joulesy just collision is found to be 10∝. Find the value of α.
The correct Answer is:50J
To solve the problem step-by-step, we will follow the reasoning presented in the video transcript while ensuring clarity and completeness.
Step 1: Understand the Problem
We have a ball of mass m=1kg projected horizontally. The kinetic energy of the ball just before it collides with the ground is given as 10α joules. We need to find the value of α.
Step 2: Determine the Velocity Just Before Collision
The ball is projected horizontally and falls from a height h=5m. The vertical velocity of the ball just before the collision can be determined using the equation of motion under gravity:
vy=√2gh
Substituting g=10m/s2 and h=5m:
vy=√2×10×5=√100=10m/s
Step 3: Calculate the Total Velocity Just Before Collision
Since the ball is projected horizontally, its horizontal velocity vx remains constant. The total velocity v just before the collision can be found using the Pythagorean theorem:
v=√v2x+v2y
Assuming the horizontal velocity vx=10m/s:
v=√(10)2+(10)2=√100+100=√200=10√2m/s
Step 4: Calculate the Kinetic Energy Just Before Collision
The kinetic energy KE of the ball just before the collision is given by:
KE=12mv2
Substituting m=1kg and v=10√2m/s:
KE=12×1×(10√2)2=12×1×200=100J
Step 5: Relate Kinetic Energy to Given Expression
According to the problem, the kinetic energy just before collision is represented as 10α:
10α=100
Step 6: Solve for α
To find α:
α=10010=10
Final Answer
The value of α is 10.
---
We have a ball of mass m=1kg projected horizontally. The kinetic energy of the ball just before it collides with the ground is given as 10α joules. We need to find the value of α.
The ball is projected horizontally and falls from a height h=5m. The vertical velocity of the ball just before the collision can be determined using the equation of motion under gravity:
Since the ball is projected horizontally, its horizontal velocity vx remains constant. The total velocity v just before the collision can be found using the Pythagorean theorem:
The kinetic energy KE of the ball just before the collision is given by:
According to the problem, the kinetic energy just before collision is represented as 10α:
To find α:
The value of α is 10.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View SolutionA ball is projected from a point O as shown in figure it will strike the ground after (g = 10 m/s2 )

View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 34th of the original. Find the coefficient of restitution.


View SolutionA ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
View SolutionA ball of mass 4 kg moving on a smooth horizontal surface makes an elastic collision with another ball of mass m at rest in the line of motion of first ball. If after collision first ball moves in the same direction with one fourth of its velocity before collision, then mass of second ball is
View SolutionA ball of mass 5 kg moving with speed 8 m/s collides head on with another stationary ball of mass 15 kg. If collision is perfectly inelastic, then loss in kinetic energ is
View SolutionTwo balls having masses m and 2m are fastened to two light strings of same length shown in the figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a). Find velocities of the balls just after their collision. (b). How high will the balls rise after the collision.

View SolutionA ball stikes a horizontal floor at an angle theta = 30° with normal to the floor . The coefficient of restitution between the ball and floor is. e=13. The percentage of its kinetic energy lost in the collision is nearly
View SolutionVelocity of the ball A after collision with the ball B as shown in the figure is (Assume perfectly inelastic and head - on collision)
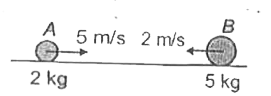
View Solution
