Consider an one dimensional elastic collision between a given incoming body A and body B, initially at rest. The mass of B in comparison to the mass of A in order that B should move with greatest kinetic energy is
mB>>mA
ma<<mA
mB=mA
can't say anything
The correct Answer is:C)
To solve the problem of determining the mass of body B in comparison to the mass of body A such that body B moves with the greatest kinetic energy after a one-dimensional elastic collision, we can follow these steps:
1. Understand the Problem:
We have two bodies, A and B. Body A has mass mA and is moving with an initial velocity u. Body B has mass mB and is initially at rest (velocity = 0). We need to find the ratio of the masses mBmA such that body B moves with the greatest kinetic energy after the collision.
2. Conservation of Momentum:
In an elastic collision, both momentum and kinetic energy are conserved. The conservation of momentum can be expressed as:
mAu+mB⋅0=mAv1+mBv2
where v1 is the final velocity of body A and v2 is the final velocity of body B.
3. Conservation of Kinetic Energy:
The conservation of kinetic energy can be expressed as:
12mAu2+0=12mAv21+12mBv22
4. Expressing Final Velocities:
For elastic collisions, we can derive the final velocities using the following formulas:
v1=mA−mBmA+mBu
v2=2mAmA+mBu
5. Kinetic Energy of Body B:
The kinetic energy of body B after the collision is given by:
KEB=12mBv22
Substituting v2:
KEB=12mB(2mAmA+mBu)2
Simplifying this, we get:
KEB=2mBm2Au2(mA+mB)2
6. Maximizing Kinetic Energy:
To maximize KEB, we can differentiate it with respect to mB and set the derivative to zero. However, we can also use a physical insight: for maximum kinetic energy transfer, body A should come to rest after the collision. This occurs when:
v1=0⟹mA−mBmA+mBu=0
This implies mA=mB.
7. Conclusion:
Therefore, for body B to move with the greatest kinetic energy after the collision, the mass of B must be equal to the mass of A:
mBmA=1
We have two bodies, A and B. Body A has mass mA and is moving with an initial velocity u. Body B has mass mB and is initially at rest (velocity = 0). We need to find the ratio of the masses mBmA such that body B moves with the greatest kinetic energy after the collision.
In an elastic collision, both momentum and kinetic energy are conserved. The conservation of momentum can be expressed as:
mAu+mB⋅0=mAv1+mBv2
where v1 is the final velocity of body A and v2 is the final velocity of body B.
The conservation of kinetic energy can be expressed as:
12mAu2+0=12mAv21+12mBv22
For elastic collisions, we can derive the final velocities using the following formulas:
v1=mA−mBmA+mBu
v2=2mAmA+mBu
The kinetic energy of body B after the collision is given by:
KEB=12mBv22
Substituting v2:
KEB=12mB(2mAmA+mBu)2
Simplifying this, we get:
KEB=2mBm2Au2(mA+mB)2
To maximize KEB, we can differentiate it with respect to mB and set the derivative to zero. However, we can also use a physical insight: for maximum kinetic energy transfer, body A should come to rest after the collision. This occurs when:
v1=0⟹mA−mBmA+mBu=0
This implies mA=mB.
Therefore, for body B to move with the greatest kinetic energy after the collision, the mass of B must be equal to the mass of A:
mBmA=1
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Consider the elastic collision f two bodies A and B of equal mass. Initially B is at rest and A moves with velocity v. After the collision -
View SolutionA body of mass m1 moving at a constant speed undergoes an elastic head on collision with a body of mass m2 initially at rest. The ratio of the kinetic energy of mass m1 after the collision to that before the collision is -
View Solution
Knowledge Check
For a given mass of a body if velocity is doubled the kinetic energy is ..........
AhalvedBfour timesC1/4thDnone of theseConsider the following statements A and B. Identify the correct choice in the given answers
A. In a one dimensional perfectly elastic collision between two moving bodies of equal masses the bodies merely exchange their velocities after collision.
B. If a lighter body at rest suffers perfectly elastic collision with a very heavy body moving with a certain velocity, then after collision both travel with same velocity.AA and B are correctBBoth A and B are wrongCA is correct, B is wrongDA is wrong, B is correct
Maximum energy transfer for an elastic collision will occur if one body is at rest when
View SolutionA body of mass m is moving with speed v makes a one-dimensional collision with a stationary body of same mass on a horizontal table . They are in connect for the a very small time interval Δt. The contact force between them varies varies as shown in the graph. ( Neglect friction)
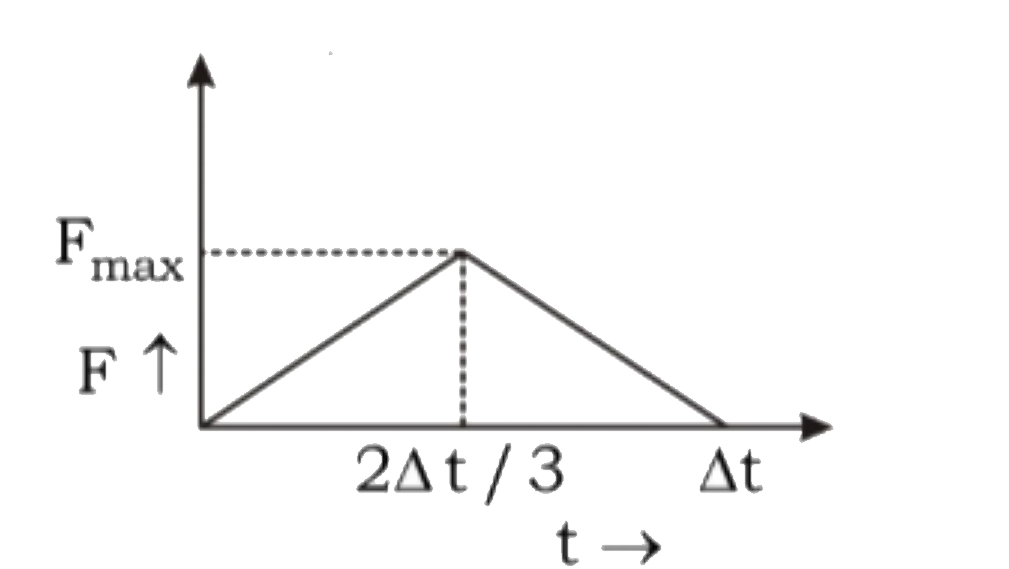
The coefficient of restitution for the collision will be
View SolutionA body of mass 2 m moving with velocity v makes a head - on elastic collision with another body of mass m which is initially at rest. Loss of kinetic energy of the colliding body (mass 2 m) is
View SolutionA moving body of mass m makes a head on elastic collision with another body of mass 2m which is initially at rest. Find the fraction of kinetic energy lost by the colliding particles after collision.
View SolutionA body 'A' moving in a straight line with velocity v makes a collision with a body 'B' initially at rest. After collision, B acquires a velocity of 1.6v. Assuming the bodies to be perfectly elastic, what is the ratio of the mass of A to that of B? What percentage of A's energy is transferred to B as a result of collision.
View SolutionA body of mass M moving with a speed u has a ‘head on’, perfectly elastic collision with a body of mass m initially at rest. If M>>m , the speed of the body of mass m after collision, will be nearly :
View Solution
