Question

A block of mass 5 kg moves from left to right with a velocity of $2m{s}^{-1}$ and collides with another block of mass 3 kg moving along the same line in the opposite direction with velocity $4m{s}^{-1}$.
(i) If the collision is perfectly elastic, determine velocities of both the blocks after their collision.
(ii) If coefficient of restitution is 0.6, determine velocities of both the blocks after their collision.

Explanation

Denoting the first block by A and the second block by B velocities immediately defore and after the impact are shown in the figure.

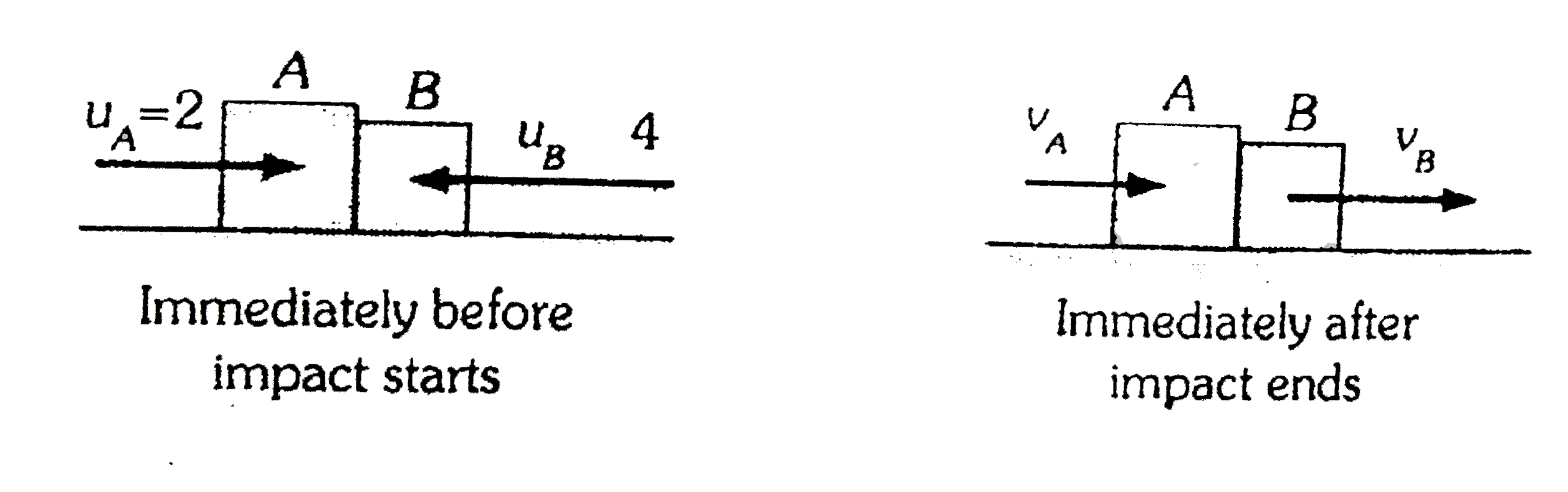
Applying principle of conservation of momentum, we have
`m_(B)v_(B) + m_(A)v_(A) = m_(A)u_(A) + m_(B)u_(b) rarr 3v_(B) + 5VA = 5 xx 2 + 3 xx (-4)`
`3v_(B) + 5v_(A) = -2` ...(i)
Applying equation of coefficient of restitution, we have `v_(B) - v_(A)= e(u_(A)-u_(B)) rarr v_(b) - v_(A) = e{2-(-4)}`
`v_(B)- v_(A) = 6e` ...(ii)
(a) For perfectly elastic impact `e=1`. using this value in equation (ii), we have
`v_(B) - v_(A) =6` ...(ii)
Now from equation (i) and(iia), we obtain
`v_(A) = -2.5 m//s` and `v_(b) = 3.5m//s`
(b) For value `e= 0.6`, equation 2 is modified as
`v_(B)-v_(A)= 3.6` ....(iib)
Now from equation (i) and (iib), we obtain
`v_(A) = - 1.6m//s` and `v_(B) = 2.0m//s`
Block A reverse back with speed 1.6 m/s and B also move in opposite direction to its original direction with speed `2.0 m//s`.