Two particles of masses 2 kg and 3 kg are moving under their mutual interaction in free space. At an instant they were observed at points(-2m,1m,4m) and(2m,-3m,6m) with velocities (3ˆi−2ˆj+ˆk)m/s and (−ˆi+ˆj−2ˆk)m/s respectively. If after 10 sec, the first particle passes the point (6m,8m,-6m), find coordinate of the point where the second particle at this instant?
To solve the problem step by step, we will follow these steps:
Step 1: Identify the Initial Conditions
We have two particles with the following properties:
- Particle 1 (mass m1=2kg):
- Initial position: r1=(−2m,1m,4m)
- Velocity: v1=(3^i−2^j+^k)m/s
- Particle 2 (mass m2=3kg):
- Initial position: r2=(2m,−3m,6m)
- Velocity: v2=(−^i+^j−2^k)m/s
Step 2: Calculate the Center of Mass Velocity
The velocity of the center of mass vcm is given by:
vcm=m1v1+m2v2m1+m2
Substituting the values:
vcm=2(3^i−2^j+^k)+3(−^i+^j−2^k)2+3
Calculating the numerator:
=(6^i−4^j+2^k)+(−3^i+3^j−6^k)5
=(3^i−j−4^k)5
Thus,
vcm=(35^i−15^j−45^k)m/s
Step 3: Calculate the Displacement of Particle 1
After 10 seconds, the position of Particle 1 is given as (6m,8m,−6m).
The initial position of Particle 1 was (−2,1,4).
Thus, the displacement Δr1 is:
Δr1=(6−(−2),8−1,−6−4)=(8,7,−10)
Step 4: Calculate the Displacement of Particle 2
Let the final position of Particle 2 be (x,y,z).
The displacement Δr2 can be expressed as:
Δr2=(x−2,y+3,z−6)
Step 5: Relate the Displacements Using the Center of Mass
Since the center of mass velocity is constant, we can relate the displacements of the two particles:
m1Δr1+m2Δr2=0
Substituting the known values:
2(8,7,−10)+3(x−2,y+3,z−6)=0
This gives us three equations:
1. 16+3(x−2)=0
2. 14+3(y+3)=0
3. −20+3(z−6)=0
Step 6: Solve for x,y,z
1. From 16+3(x−2)=0:
3(x−2)=−16⟹x−2=−163⟹x=2−163=−103
2. From 14+3(y+3)=0:
3(y+3)=−14⟹y+3=−143⟹y=−143−3=−233
3. From −20+3(z−6)=0:
3(z−6)=20⟹z−6=203⟹z=6+203=383
Final Answer
The coordinates of Particle 2 after 10 seconds are:
(−103,−233,383)
We have two particles with the following properties:
- Particle 1 (mass m1=2kg):
- Initial position: r1=(−2m,1m,4m)
- Velocity: v1=(3^i−2^j+^k)m/s
- Initial position: r2=(2m,−3m,6m)
- Velocity: v2=(−^i+^j−2^k)m/s
The velocity of the center of mass vcm is given by:
vcm=m1v1+m2v2m1+m2
Substituting the values:
vcm=2(3^i−2^j+^k)+3(−^i+^j−2^k)2+3
Calculating the numerator:
=(6^i−4^j+2^k)+(−3^i+3^j−6^k)5
=(3^i−j−4^k)5
Thus,
vcm=(35^i−15^j−45^k)m/s
After 10 seconds, the position of Particle 1 is given as (6m,8m,−6m).
The initial position of Particle 1 was (−2,1,4).
Thus, the displacement Δr1 is:
Δr1=(6−(−2),8−1,−6−4)=(8,7,−10)
Let the final position of Particle 2 be (x,y,z).
The displacement Δr2 can be expressed as:
Δr2=(x−2,y+3,z−6)
Since the center of mass velocity is constant, we can relate the displacements of the two particles:
m1Δr1+m2Δr2=0
Substituting the known values:
2(8,7,−10)+3(x−2,y+3,z−6)=0
This gives us three equations:
1. 16+3(x−2)=0
2. 14+3(y+3)=0
3. −20+3(z−6)=0
1. From 16+3(x−2)=0:
3(x−2)=−16⟹x−2=−163⟹x=2−163=−103
3(y+3)=−14⟹y+3=−143⟹y=−143−3=−233
3(z−6)=20⟹z−6=203⟹z=6+203=383
The coordinates of Particle 2 after 10 seconds are:
(−103,−233,383)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A particle A moves with velocity (2ˆi−3ˆj)m/s from a point (4,5m)m. At the same instant a particle B, moving in the same plane with velocity(4ˆi+ˆj)m/s passes through a point C(0,−3)m. Find the x-coordinate (in m) of the point where the particles collide.
View SolutionArea of a parallelogram formed by vectors (3ˆi−2ˆj+ˆk)m and (ˆi+2ˆj+3ˆk) m as adjacent sides is
View SolutionA body starts with a velocity 2ˆi+3ˆj+11ˆkm/s and moves with an acceleration 10ˆi+10ˆj+10ˆkm/s2. What is its velocity after 0.2 seconds ?
View SolutionThe initial and final position vector for a particle are(-3m) ˆi+(2m)ˆj+(8m)ˆk and (9m)ˆi+(2m)ˆj+(−8m)ˆk respectively ,find the displacement of the particle.
View SolutionVelocity and acceleration of a particle at time t=0are u=(2ˆi+3ˆj)m/sanda=(4ˆi+3ˆj)m/s2 respectively. Find the velocity and displacement if particle at t=2s.
View SolutionVelocity vectors of three masses 2kg,1kg and 3 kg are →v1=(ˆi−2ˆj+ˆk)ms,→V2=(2ˆi+2ˆj−ˆk)ms and →v3 respectively. If velocity vector of center of mass of the system is zero then value of →v3 will be
View SolutionFind the Vab in an electric field E=(2ˆi+3ˆj+4ˆk)NC, where ra=(ˆi−2ˆj+ˆk)m and rb=(2ˆi+ˆj−2ˆk)m
View SolutionA particle of mass 2kg is moving in free space with velocity →v0=(2ˆi−3ˆj+ˆk)m/s is acted upon by force →F=(2ˆi+ˆj−2ˆk)N. Find velocity vector of the particle 3s after the force starts acting.
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
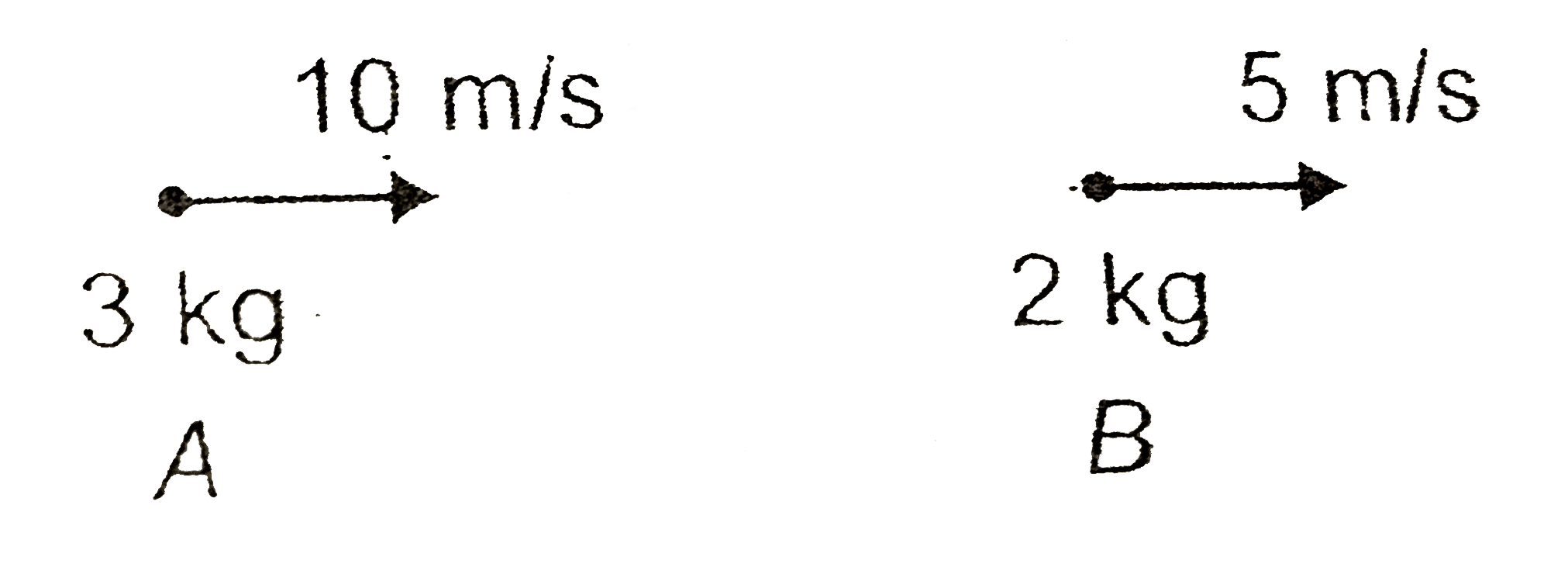
Find the maximum momentum that particle B can have after collision with A
View SolutionThe position vector of three particles of masses m1=1kg.
m2=2kg and m3=3kg are r1=(ˆi+4ˆj+ˆk)m, r2=(ˆi+ˆj+ˆk)m and r3=(2ˆi−ˆj−2ˆk)m respectively. Find the position vector of their centre of mass.
View Solution

