Find coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
To find the coordinates of the center of mass of a non-uniform rod of length L with a linear mass density given by λ=a+bx, where x is the distance from the lighter end, we can follow these steps:
Step 1: Define the mass element
The linear mass density is given as:
λ(x)=a+bx
To find the mass element dm for a small segment dx of the rod, we can express it as:
dm=λ(x)dx=(a+bx)dx
Step 2: Total mass of the rod
The total mass M of the rod can be found by integrating dm over the length of the rod from 0 to L:
M=∫L0dm=∫L0(a+bx)dx
Calculating this integral:
M=∫L0(a+bx)dx=(ax+b2x2)L0=aL+b2L2
Step 3: Calculate the moment about the origin
To find the x-coordinate of the center of mass xcm, we use the formula:
xcm=1M∫L0xdm
Substituting dm:
xcm=1M∫L0x(a+bx)dx
Calculating this integral:
∫L0x(a+bx)dx=∫L0(ax+bx2)dx=(a2x2+b3x3)L0=a2L2+b3L3
Step 4: Substitute into the center of mass formula
Now we can substitute back into the formula for xcm:
xcm=1M(a2L2+b3L3)
Substituting M:
xcm=1aL+b2L2(a2L2+b3L3)
Step 5: Simplify the expression
Now we simplify the expression:
xcm=3aL2+2bL36aL+3bL2
This gives us the x-coordinate of the center of mass.
Final Result
Thus, the coordinates of the center of mass of the rod are:
xcm=3aL+2bL23(2a+bL)
The linear mass density is given as:
λ(x)=a+bx
To find the mass element dm for a small segment dx of the rod, we can express it as:
dm=λ(x)dx=(a+bx)dx
The total mass M of the rod can be found by integrating dm over the length of the rod from 0 to L:
M=∫L0dm=∫L0(a+bx)dx
Calculating this integral:
M=∫L0(a+bx)dx=(ax+b2x2)L0=aL+b2L2
To find the x-coordinate of the center of mass xcm, we use the formula:
xcm=1M∫L0xdm
Substituting dm:
xcm=1M∫L0x(a+bx)dx
Calculating this integral:
∫L0x(a+bx)dx=∫L0(ax+bx2)dx=(a2x2+b3x3)L0=a2L2+b3L3
Now we can substitute back into the formula for xcm:
xcm=1M(a2L2+b3L3)
Substituting M:
xcm=1aL+b2L2(a2L2+b3L3)
Now we simplify the expression:
xcm=3aL2+2bL36aL+3bL2
This gives us the x-coordinate of the center of mass.
Thus, the coordinates of the center of mass of the rod are:
xcm=3aL+2bL23(2a+bL)
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-I
Explore 40 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-II
Explore 43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
The centre of mass of a non-uniform rod of length L whose mass per unit length λ is proportional to x2, where x is distance from one end
View SolutionThe centre of mass of a non uniform rod of length L, whose mass per unit length varies as ρ=k.x2L where k is a constant and x is the distance of any point from one end is (from the same end)
View SolutionThere is a rod of length l , its density varies with length as distance of λ=ax , where x is distance from left end. Find center of mass from left end.
View SolutionA heavy metallic rod of non-uniform mass distribution, is hanged vertically from a rigid support. The linear mass density varies as λ(x)=k×x where x is the distance measured along the length of rod, from its lower end. Find extension in rod due to its own weight.
View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionThe adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is αA and in the second case it is αB then
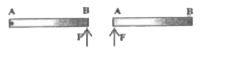
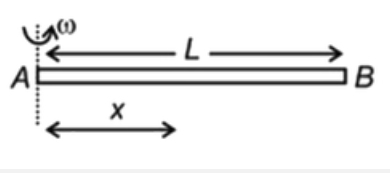
View SolutionA non - conducting rod of length L with linear charge density λ=λ0x where x is the distance from end A is rotating with constant angular speed ω about the same end. If the angular velocity of the rod (ω) is large, then the magnetic dipole moment of the system is ωλ0L4n. What is the value of n?
View SolutionA rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?

View SolutionFind the x coordinate of the centre of mass of the non - uniform rod of length L givne below. The origin is taken at the left end of the rod. The density of the rod as a function of its x- coordinates is ρ=ax2+bx+c, where a, b and c are constants.

View SolutionThe linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View Solution

