In a certain region of space, the gravitational field is given by −kr where r is the distance and k is a constant. If the gravitaional potential at r=r0 be V0, then what is the expression for the gravitaional potential (V)-
klog(rr0)
klog(r0r)
V0+klog(rr0)
V0+klog(r0r)
The correct Answer is:D
To find the expression for the gravitational potential V given the gravitational field E=−kr, we can follow these steps:
1. Understand the relationship between gravitational field and potential:
The gravitational field E is related to the gravitational potential V by the equation:
E=−dVdr
This means that the gravitational field is the negative gradient (rate of change) of the gravitational potential.
2. Substitute the given gravitational field:
We know that the gravitational field in this case is given by:
E=−kr
Therefore, we can write:
−dVdr=−kr
This simplifies to:
dVdr=kr
3. Integrate to find the potential:
To find V, we need to integrate dVdr:
dV=krdr
Integrating both sides gives:
V=klnr+C
where C is the constant of integration.
4. Determine the constant of integration:
We are given that the gravitational potential at r=r0 is V0. Therefore, we can use this condition to find C:
V0=klnr0+C
Rearranging gives:
C=V0−klnr0
5. Substitute back to find the expression for V:
Now, substituting C back into the expression for V:
V=klnr+(V0−klnr0)
This simplifies to:
V=V0+kln(rr0)
Final Expression:
Thus, the expression for the gravitational potential V is:
V=V0+kln(rr0)
The gravitational field E is related to the gravitational potential V by the equation:
E=−dVdr
This means that the gravitational field is the negative gradient (rate of change) of the gravitational potential.
We know that the gravitational field in this case is given by:
E=−kr
Therefore, we can write:
−dVdr=−kr
This simplifies to:
dVdr=kr
To find V, we need to integrate dVdr:
dV=krdr
Integrating both sides gives:
V=klnr+C
where C is the constant of integration.
We are given that the gravitational potential at r=r0 is V0. Therefore, we can use this condition to find C:
V0=klnr0+C
Rearranging gives:
C=V0−klnr0
Now, substituting C back into the expression for V:
V=klnr+(V0−klnr0)
This simplifies to:
V=V0+kln(rr0)
Thus, the expression for the gravitational potential V is:
V=V0+kln(rr0)
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)
20 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 4 A (Conceptual Subjective Exercise)
14 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 1 (Check your Grasp)
28 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
In a certain region of space, the potential is given by V=k(2x2−y2+z2). The electric field at the point (1, 1, 1) has magnitude:
View SolutionLet gravitation field in a space be given as E=−(k/r) If the reference point is a distance d where potential is V1 then relation for potential is .
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionIf the gravitational field intensity at a point is given by g=GMr2.5. Then, the potential at a distance r is
View SolutionIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
View SolutionThe potential energy of a two particle system separated by a distance r is given by U(r)=Ar where A is a constant. Find to the radial force Fr, that each particle exerts on the other.
View SolutionPotential energy in a field is given by U=−Ar6+Br11 then find the value of r for equilibrium position.
View SolutionA conservative force held function is given by F=k/r2, where k is a constant.
a. Determine the potential energy funciton U(r) assuming zero potential energy at r=r0.
b. Also, determine the potential energy at r=∞.
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
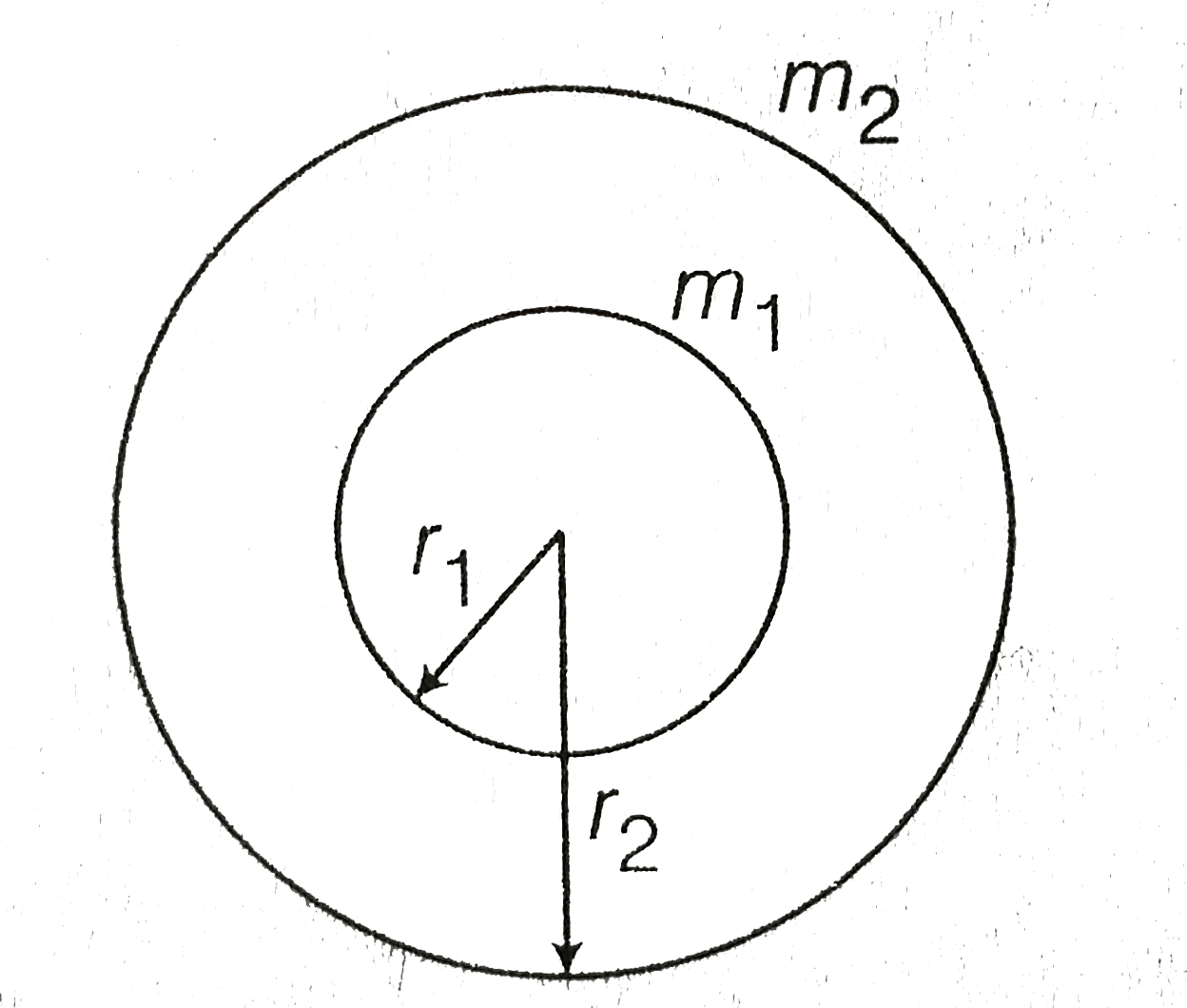
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View Solution
