A conservative force held function is given by , where k is a constant.
a. Determine the potential energy funciton assuming zero potential energy at .
b. Also, determine the potential energy at .
To solve the problem step by step, we will follow the instructions given in the video transcript and apply the relevant physics concepts.
Part a: Determine the potential energy function U(r)
1. Understand the relationship between force and potential energy:
The relationship between a conservative force F and the potential energy U is given by:
F=−dUdr
Given that F=kr2, we can express this as:
−dUdr=kr2
2. Rearranging the equation:
Rearranging gives:
dUdr=−kr2
3. Integrate to find U(r):
To find U(r), we integrate with respect to r:
U(r)=−∫kr2dr
The integral of 1r2 is −1r, so we have:
U(r)=−k(−1r)+C=kr+C
where C is the constant of integration.
4. Determine the constant C:
We are given that the potential energy is zero at r=r0:
U(r0)=0⟹kr0+C=0⟹C=−kr0
5. Final expression for U(r):
Substituting C back into the equation for U(r):
U(r)=kr−kr0
Part b: Determine the potential energy at r=∞
1. Substituting r=∞:
We need to find U(∞):
U(∞)=k∞−kr0
Since k∞=0, we have:
U(∞)=0−kr0=−kr0
Summary of Results
- The potential energy function is:
U(r)=kr−kr0
- The potential energy at r=∞ is:
U(∞)=−kr0
The relationship between a conservative force F and the potential energy U is given by:
F=−dUdr
Given that F=kr2, we can express this as:
−dUdr=kr2
Rearranging gives:
dUdr=−kr2
To find U(r), we integrate with respect to r:
U(r)=−∫kr2dr
The integral of 1r2 is −1r, so we have:
U(r)=−k(−1r)+C=kr+C
where C is the constant of integration.
We are given that the potential energy is zero at r=r0:
U(r0)=0⟹kr0+C=0⟹C=−kr0
Substituting C back into the equation for U(r):
U(r)=kr−kr0
We need to find U(∞):
U(∞)=k∞−kr0
Since k∞=0, we have:
U(∞)=0−kr0=−kr0
- The potential energy function is:
U(r)=kr−kr0
- The potential energy at r=∞ is:
U(∞)=−kr0
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Solved Examples
Explore 15 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
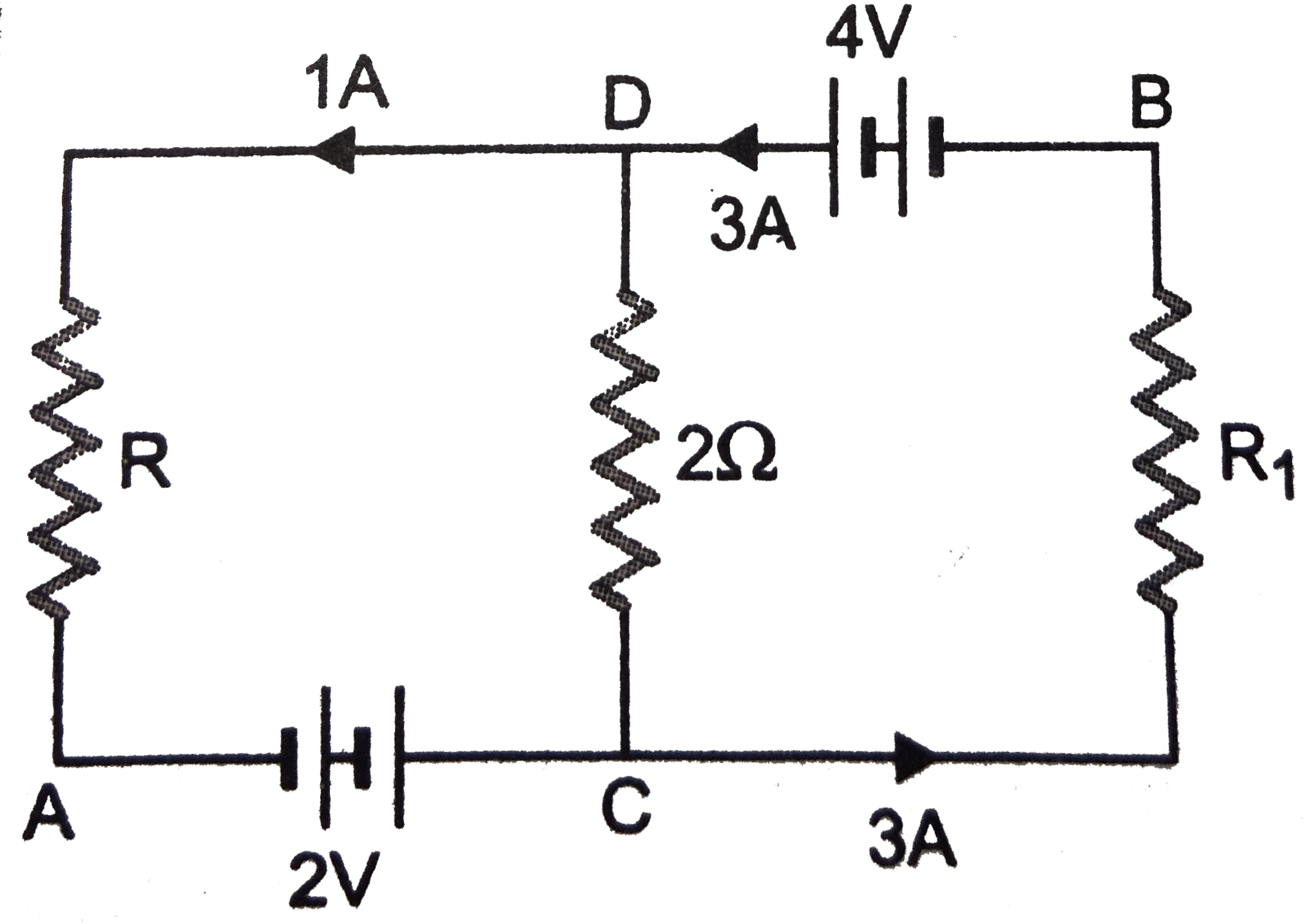
In the given circuit assuming poiny A to at zero potential use kirchhoff's rules to determine the potential at point B
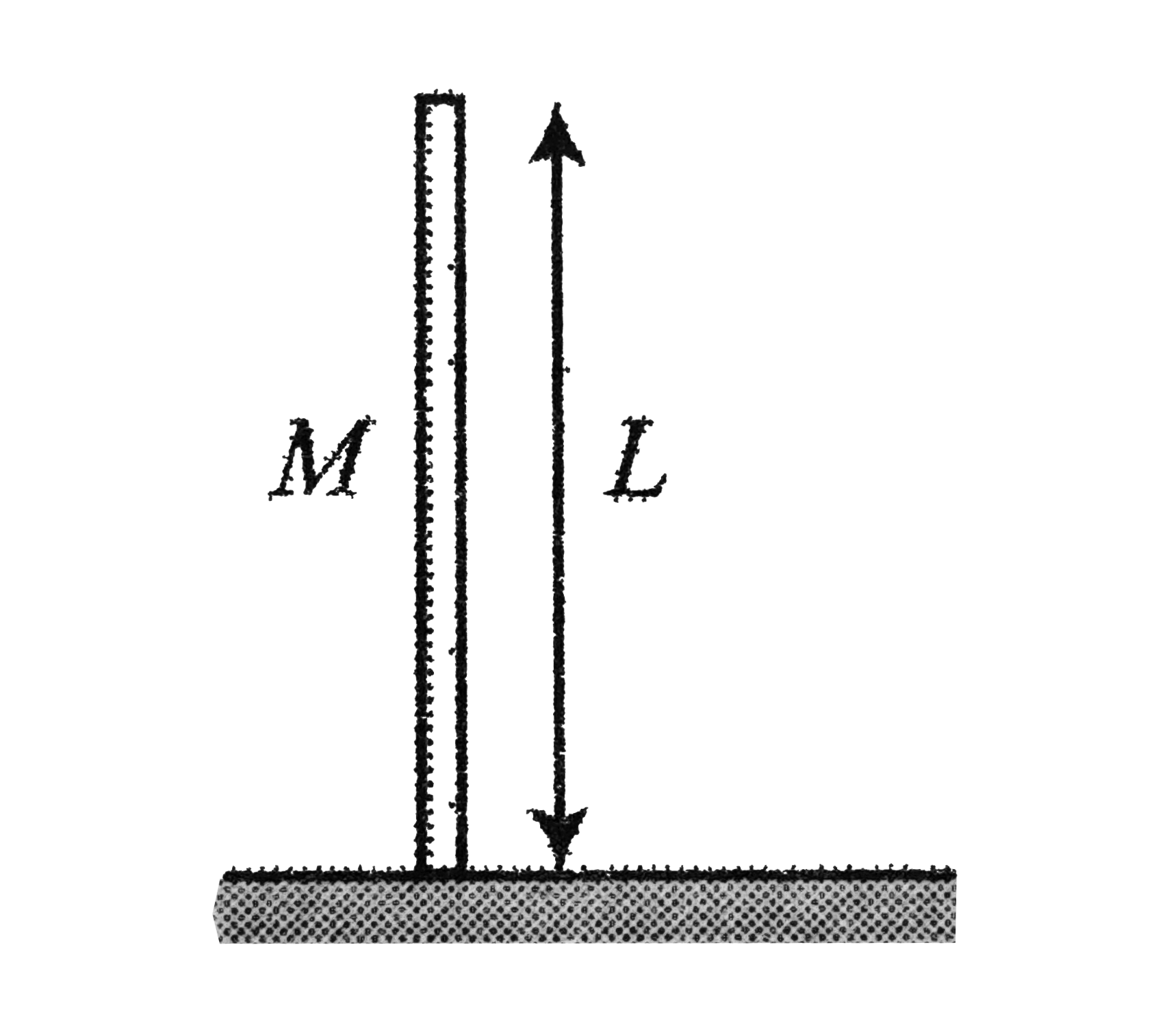
View SolutionA uniform rod of mass M and length L is held vertically upright on a horizontal surface as shown in figure. Assuming zero potential energy at the base of the rod, determine the potential energy of the rod.
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
If the total energy of the particle is E=−3B216A, and it is known that the motion is radial only then the velocity is zero at
View Solutionif the potential energy of a hydrogen atom in the ground state is assumed to be zero, then total energy of n=∞ is equal to
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium distance is given by
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium is
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity is
View SolutionThe potential energy for a conservative force system is given by U=ax2−bx. Where a and b are constants find out (a) The expression of force (b) Potential energy at equilibrium.
View SolutionThe potential energy for a conservative force system is given by U=ax2−bx. Where a and b are constants find out (a) The expression of force (b) Potential energy at equilibrium.
View SolutionAssuming that potential energy of spring is zero when it is stretched by x02, its potential energy when it is compressed by x0 is
View Solution

