Show mathematically that the potential at a point on the equitorial line of an electic dipole is zero.Solution in Punjabi
Electric Potential at any point due to an Electric Dipole : Consider an electric dipole AB having charge - 9 at point A and charge + q at point B and 2a is its dipole length. Let O be the centre of the dipole and P be any point at a distance from its centre, where electric potential due to the dipole is to be determined. Let ∠POB=θ.
The potential at point P due to charge -q,
and the potential at point P due to charge +q,
V2=14π∈0.qPB
Therefore, net potential at point P due to the dipole,
V2=V1+V2=−14π∈0.qPA+14π∈0.qPB
or V=14π∈0.q[1PB−1PA] ......(i)
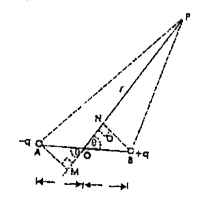
To find PB and PA, draw BN perpendicular to OP and AM perpendicular to PQ after producing it. From right angled AAMO, we have
cosθ=OMOA=OMaorOM=acosθ
In case the length of the dipole is very small as compared to distance r, then PA≈PM=PO+OM=r÷acos
Similarly, it can be obtained that
PB=r−acosθ
In the equation (1), substituting for PA and PB, we have
V=14π∈0.q[1r−acosθ−1r+acosθ]
=14π∈0.q[r+acosθ−r+acosθr2−a2cos2θ]
=14π∈0.q[2acosθr2−a2cos2θ]
Since q (20) = P, the electric dipole moment of the dipole, the above equation becomes
V=14π∈0.Pcosθ(r2−a2cos2θ) ......(2)
The equation (2) gives electric potential due to the dipole at a distance r from its centre in a direction making an angle with the dipole.
Special cases : Let us find the electric potential due to the dipole in the following two cases :
When point P lies on the axial line of the dipole :
In such a case, θ=0∘ and cos0∘=1
Therefore, the equation (2) gives
V=14π∈0.Pcos0∘(r2−a2cos20∘)
V=14π∈0.P(1)(r2−a2)
V=14π∈0.P(r2−a2)
When point P lies on the equitorial line of the dipole :
In such a case, theta=90^(@).andcos90^(@)=0
From equation (2)
y=0
Topper's Solved these Questions
- ELECTROSTATIC POTENTIALBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - NUMERICAL PROBLEMS
16 Videos
- ELECTROSTATIC POTENTIALBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - MOST EXPECTED QUESTIONS
7 Videos
- ELECTROSTATIC POTENTIALBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - SHORT ANSWERTYPE QUESTIONS (2 Marks Questions)
9 Videos
- ELECTRONIC DEVICES SOLIDSBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRONIC DEVICES SOLIDSEXERCISE - Most Expected Questions
9 Videos
- FORCE ON A CHARGE BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CHARGE EXERCISE - NUMERICAL PROBLEMS
14 Videos
Similar Questions
Two charges 3×10−8Cand−2×10−8C are located 15 cm apart. At what point on the line joining the two charges is the electrical potential zero? Take the potential at infinity to be zero.
View SolutionName the physical quantity whose SI unit is volt metre−1.
View SolutionHow can the whole charge of a conductor be transferred to another isolated conductor?
View SolutionWhy semiconductors are doped?
View SolutionAn electron (with charge 1.6×10−19C) moving at right angles to a uniform magnetic field completes a circular orbit in 10−6sec. Calculate the vlaue of magnetic field. Given mass of electron =9×10−31kg.
View SolutionDerive a relation for electric field of an electric dipole at a point on its equitorial line.
View SolutionShow mathematically that the potential at a point on the equatorial line of an electric dipole is zero.
View SolutionObtain an expression for electric field intensity at any point on equitorial line of electric dipole. What is the direction of electric field?
View SolutionWhat is magnetic dipole? Derive an expression for magnetic field intensity at a point on the equitorial line of a bar magnet.
View SolutionDipole And Dipole Moment|Electric Field At Axial Point Of Dipole|Electric Field At Equitorial Point Of Dipole|Examples
View SolutionPotential Due To Point Charge|Potential Due To System Of Point Charge|Potential At Axial Point Of Dipole |Potential At Equitorial Point Of Dipole
View SolutionIn an electric dipole, at which point is the electric potential zero?
View SolutionElectric potential due to an electric dipole is zero at a point on the………. Line.
View SolutionDefine an electrostatic potential. What are its unit and dimensions ? Show that the potential at a point on the equatorial line of a dipole is zero.
View SolutionWhat is the direction of electric field at a point on the equitorial line of electric dipole ?
View SolutionWhat is the direction of electric field at a point on the equitorial line of electric dipole ?
View Solution
