Show that work done in moving an electric charge between any two points in the electric field of a point charge is independent of the path along which the charge moves.Solution in Punjabi
Consider a point charge +q located at the origin O. The electric field due to the point charge will be directed along the dotted arrows i.e, radially outwards from the point charge +q. Suppose that AB is any path (straight or curved) between two points A and B in the electric field of the point charge +q, such that OA=rA and OB=rB. Further, suppose that P is any point on the path AB and →E is electric field due to the point charge f g at this point.
Let distance of point P from the point charge + q is OP=r. Let −−→PQ=→dl be very small displacement along the path AB. Since electric field →E gives measure of force on a unit positive charge placed at point P,
→E.→dl= work done by the electric field →E in moving a unit positive charge from point P to Qi.e., through −−→PQ.(→dl)
∫BA→E.→dl= work done by the electric field →E in moving a unit positive charge from the point A to B.
∫BA→E.→dl is called the line integral of the electric field →E between the points A and B. now find the value of integral ∫BA→E.→dl.
Electric field at point P due to point charge +q located at the point O is given
→E=14π∈0.qr2ˆr
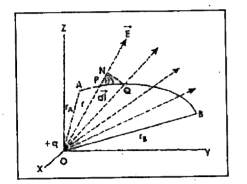
where ˆr is a unit vector along the line OP. If θ is angle between the direction of →E and →dl
→E.→dl=14π∈0.qr2ˆr.→dl=14π∈0.qr2(1)(dl)cosθ
or →E.→dl=14π∈0.qr2(dl)cosθ ......(1)
From point Q, drop ON perpendicular to OP. Then, from right angled ΔPNQ, we have
PN=PQcosθ=dlcosθ
Further, as PN (the projection of →dl along the line OP) is in the direction of increasing r, the distance PN is taken as + dr. Therefore,
dlcosθ=→dr
setting dlcosθ=dr in equation (1), we have
→E.→dl=14π∈0qr2dr
Hence, ∫BA→E.→dl=∫BA14π∈0.qr2dr=14π∈0.q∫BAr−2dr .....(2)
The values of r corresponding to points A and B are rA and rB respectively. Therefore, in equation (2) corresponding to the limits from A to B, the proper limits of integration are from rB to rB. Likewise, equation (2) becomes
∫BA→E.→dl=14π∈0.q∫rBrAr−2dr=14π∈0q∣∣∣r−1−1∣∣∣rBrB=14π∈0q∣∣∣−1r∣∣∣rBrA
=14π∈0.q∣∣∣−1rB−(−1rA)∣∣∣
or ∫BA→E.→dl=14π∈0.q(1rA−1rB) ......(3)
The equation (3) gives the value of line integral of the electric field between two points and B along the path AB shown in Fig. above. It follows that the expression depends only on the distances of the end points A and B (i.e., rA and rB ) and not upon the path AB.
Hence, the line integral of the electric field between two points is same for all the paths between the two points i.e., it is independent of the path followed between the two points.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIALBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - NUMERICAL PROBLEMS
16 Videos
- ELECTROSTATIC POTENTIALBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - MOST EXPECTED QUESTIONS
7 Videos
- ELECTROSTATIC POTENTIALBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - SHORT ANSWERTYPE QUESTIONS (2 Marks Questions)
9 Videos
- ELECTRONIC DEVICES SOLIDSBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRONIC DEVICES SOLIDSEXERCISE - Most Expected Questions
9 Videos
- FORCE ON A CHARGE BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CHARGE EXERCISE - NUMERICAL PROBLEMS
14 Videos
Similar Questions
Two charges 3×10−8Cand−2×10−8C are located 15 cm apart. At what point on the line joining the two charges is the electrical potential zero? Take the potential at infinity to be zero.
View SolutionName the physical quantity whose SI unit is volt metre−1.
View SolutionHow can the whole charge of a conductor be transferred to another isolated conductor?
View SolutionWhy semiconductors are doped?
View SolutionAn electron (with charge 1.6×10−19C) moving at right angles to a uniform magnetic field completes a circular orbit in 10−6sec. Calculate the vlaue of magnetic field. Given mass of electron =9×10−31kg.
View SolutionIf a small charge q is moved along a closed path in the field between the plates of a parallel plate capacitor, will any work be done by the agent that moves the charge?
View SolutionAssertion: Work done in moving a charge between any two points in a unifrom electric field is independent of the path followed by the charge, between these points.
Reason: Electrostatic forces are non-conservative.
View SolutionA point charge Q is moved along a ciruclar path around another fixed point charge. The work done is zero
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J . What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View SolutionThe work done in moving a charge particle between two points in a uniform electric field, does not depend on the path followed by the particle . Why ?
View Solutionअभिकथन: किसी विद्युत क्षेत्र में किन्हीं दो बिन्दुओं के बीच आवेश की गति करने में किया गया कार्य उन बिन्दुओं के मध्य, आवेश द्वारा चले गये पथ पर निर्भर नहीं करता है।
तर्क: स्थिरवैद्युत बल एक असंरक्षी बल होता है।
View SolutionA test charge q is made to move in the electric field of a point charge +Q along a closed path as shown in figure. What is the work done ?
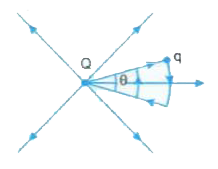
View SolutionA point charge is taken from a point A to a pint B in an electric field. Does the work done by the electric field depend on the path of the charge ?
View SolutionAssertion: Work done in moving a charge between any two points in a unifrom electric field is independent of the path followed by the charge, between these points.
Reason: Electrostatic forces are non-conservative.
View SolutionAssertion : the net work done by an electrostatic field on a charge whilr moving it from one point to another is independent of path. Reason: the net work done by an electrostatic force on a charge in it moving along a closed loop is zero.
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J. What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View Solution
