A ray of light incident on a glass sphere (refractive index √3 ) suffers total internal reflection before emerging out exactly parallel to the incident ray. The angle of incidence was
75∘
30∘
45∘
60∘
The correct Answer is:D
To solve the problem, we need to determine the angle of incidence (I) for a ray of light incident on a glass sphere with a refractive index of √3, which undergoes total internal reflection and emerges parallel to the incident ray.
1. Understanding the Geometry:
- A ray of light is incident on a glass sphere. When it enters the sphere, it refracts towards the normal due to the higher refractive index of glass compared to air.
- After some internal reflection, it emerges parallel to the incident ray.
2. Identifying Angles:
- Let the angle of incidence be I and the angle of refraction be R.
- According to the problem, the ray undergoes total internal reflection, which means that the angle of incidence inside the sphere (when it reflects) is equal to the critical angle.
3. Using Snell's Law:
- Snell's Law states that:
sinIsinR=n
- Here, n is the refractive index of the glass sphere, which is given as √3.
4. Applying the Total Internal Reflection Condition:
- For total internal reflection, we have:
I=2R
- This means the angle of incidence I is twice the angle of refraction R.
5. Substituting into Snell's Law:
- We can substitute I=2R into Snell's Law:
sin(2R)sinR=√3
- Using the double angle formula, sin(2R)=2sinRcosR, we get:
2sinRcosRsinR=√3
- Simplifying this gives:
2cosR=√3
6. Solving for R:
- Rearranging gives:
cosR=√32
- The angle R that satisfies this is:
R=30∘
7. Finding the Angle of Incidence I:
- Since I=2R:
I=2×30∘=60∘
Final Answer:
The angle of incidence I is 60∘.
---
- A ray of light is incident on a glass sphere. When it enters the sphere, it refracts towards the normal due to the higher refractive index of glass compared to air.
- After some internal reflection, it emerges parallel to the incident ray.
- Let the angle of incidence be I and the angle of refraction be R.
- According to the problem, the ray undergoes total internal reflection, which means that the angle of incidence inside the sphere (when it reflects) is equal to the critical angle.
- Snell's Law states that:
sinIsinR=n
- Here, n is the refractive index of the glass sphere, which is given as √3.
- For total internal reflection, we have:
I=2R
- This means the angle of incidence I is twice the angle of refraction R.
- We can substitute I=2R into Snell's Law:
sin(2R)sinR=√3
- Using the double angle formula, sin(2R)=2sinRcosR, we get:
2sinRcosRsinR=√3
- Simplifying this gives:
2cosR=√3
- Rearranging gives:
cosR=√32
- The angle R that satisfies this is:
R=30∘
- Since I=2R:
I=2×30∘=60∘
The angle of incidence I is 60∘.
Topper's Solved these Questions
- QUESTION PAPER 2013Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2013Exercise:PART-II ( PHYSICS)
Explore 10 Videos
- QUESTION PAPER 2013Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2013Exercise:PART-II (PHYSICS)
Explore 5 Videos
- MOCK TEST 9Book:KVPY PREVIOUS YEARChapter:MOCK TEST 9Exercise:EXERCISE
Explore 19 Videos
- QUESTION PAPER 2020Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2020Exercise:PART-I : PHYSICS
Explore 50 Videos
Similar Questions
A ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?

View Solution
Knowledge Check
A ray of light falls normally on one face of a right angled prims of refracting angle A. It suffers two total internal reflections before coming out of prism parallel to incident ray as shown. Refractive index to prism material will be:
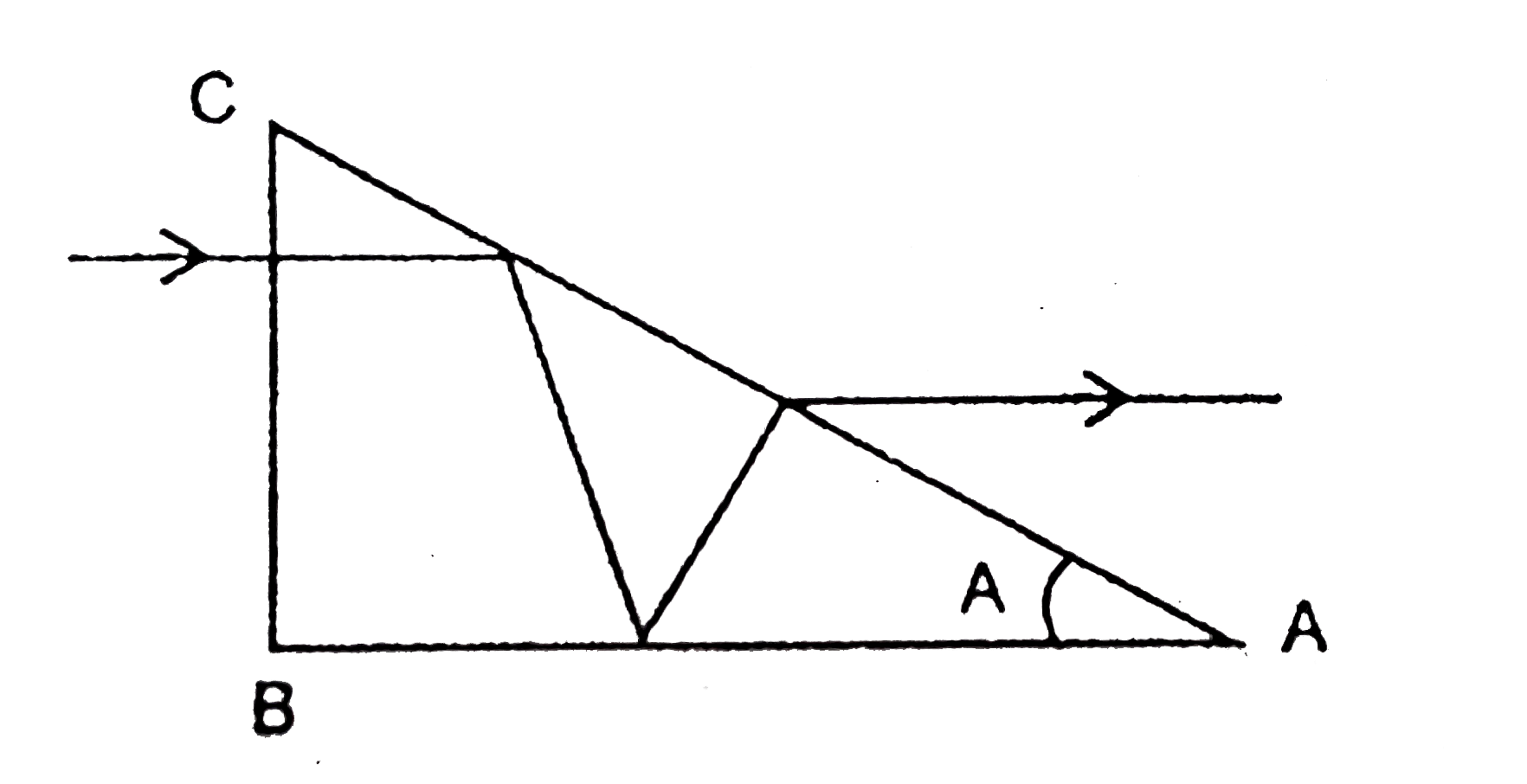 AsinAsin3ABsinAcos3ACcosAsineADcosAcos3A
AsinAsin3ABsinAcos3ACcosAsineADcosAcos3AA ray of light is incident on a glass plate. The light ray travels distance of 5 cm inside the glass plate before emerging out of the glass plate. If the incident ray suffers a deviation of 30°, the perpendicular distance between incident and the emergent ray is
A5cmB2.5cmC7.5cmD10cm
A ray of light is incident on a transparent glass slab of refractive index 1.62. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence ? [tan–1(1.62)=58.3∘]
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face ? The refractive index of the material of the prism is 1.524.
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA ray of light is incident on the surface of a glass plate of reflective index 1.536 such that the reflected and refracted rays are mutually perpendicular. What is the angle of reflection ?
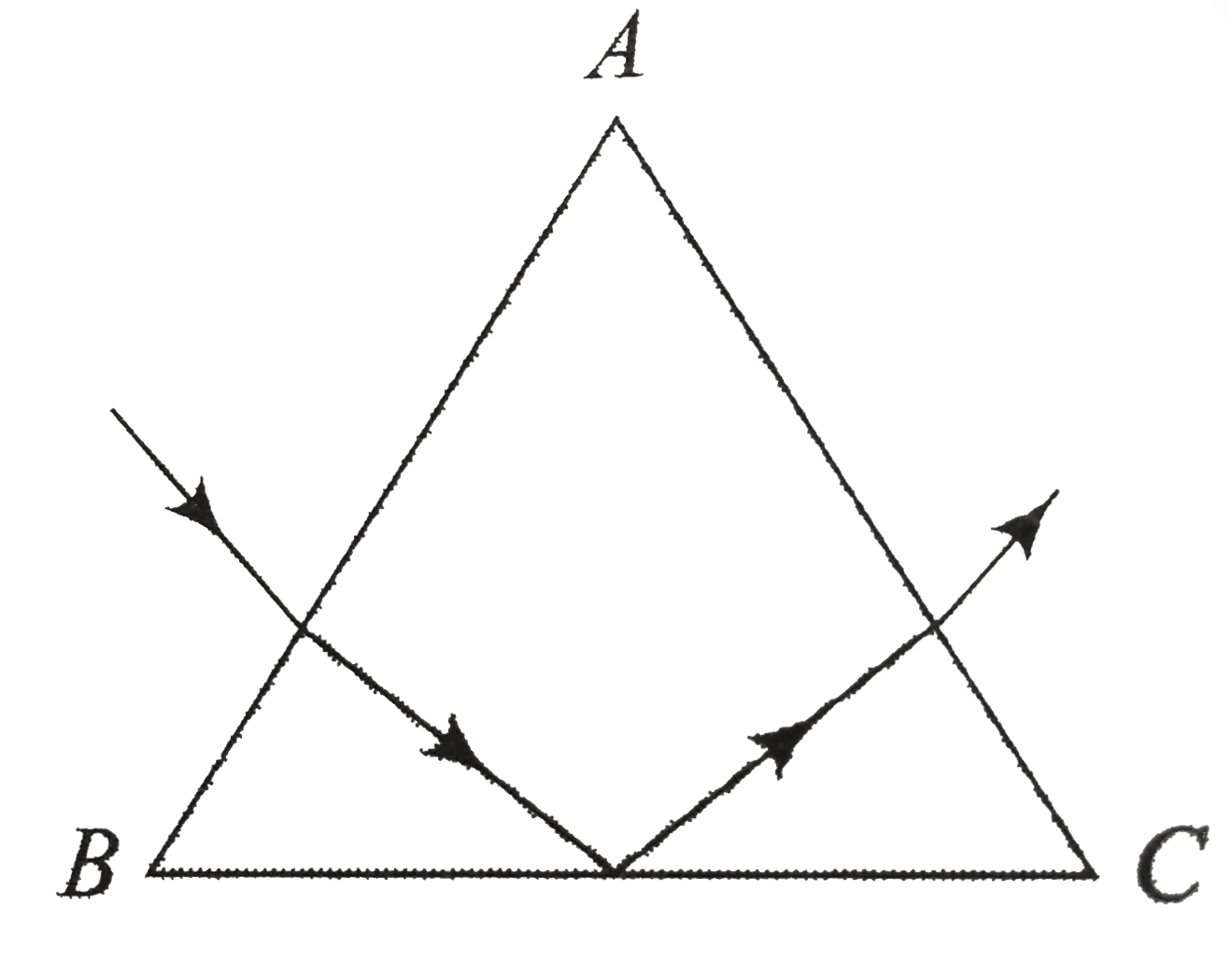
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘, so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View Solution