The bulk modulus of a gas is defined as B = -VdP/dV. For an adiabatic process the variation of B is proportional to Pn. For an idea gas, n is
0
1
52
2
The correct Answer is:B
To solve the problem, we start with the definition of the bulk modulus B for a gas:
B=−VdPdV
For an adiabatic process, we know that the volume V is proportional to the pressure P raised to the power n. This can be expressed mathematically as:
V∝PnorV=kPn
where k is a constant.
Step 1: Use the adiabatic condition
For an adiabatic process, we have the relation:
PVγ=constant
where γ is the heat capacity ratio Cp/Cv.
Step 2: Differentiate the adiabatic condition
We differentiate the equation PVγ=constant with respect to V:
ddV(PVγ)=0
Using the product rule, we get:
Pd(Vγ)dV+VγdPdV=0
Calculating d(Vγ)dV:
d(Vγ)dV=γVγ−1
Substituting this back into our differentiated equation gives:
P⋅γVγ−1+VγdPdV=0
Step 3: Rearranging the equation
Rearranging the equation yields:
VγdPdV=−P⋅γVγ−1
Dividing both sides by Vγ:
dPdV=−γPV
Step 4: Substitute into the bulk modulus equation
Now we substitute dPdV into the bulk modulus equation:
B=−V(−γPV)=γP
Step 5: Relate bulk modulus to pressure
From our derivation, we see that:
B∝P
This indicates that the bulk modulus B is directly proportional to P1.
Step 6: Conclusion
Thus, we can conclude that for an ideal gas undergoing an adiabatic process, the value of n is:
1
Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( PHYSICS)
10 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II (PHYSICS)
5 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
19 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-I : PHYSICS
50 Videos
Similar Questions
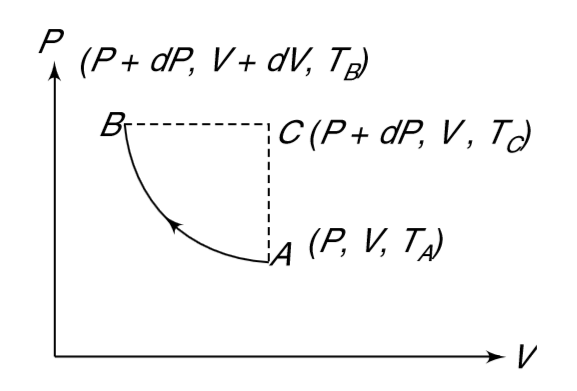
One mole of a gas is in state A[P,V,TA]. A small adiabatic process causes the state of the gas to change to B[P+dP,V+dV,TB]. The changes dV & dP are infinitesimally small and dV is negative. An alternative process takes the gas from state A to B via A→C→B. A→C is isochoric and C→B is isobaric path. State at C is [P+dP,V,TC].
(a) Rank the temperatures TA,TB and TC from highest to lowest.
(b) Find g of the gas in terms of TA, TB and TC.
View SolutionDuring an adiabatic process, the density of a gas is foung to be proportional to cube of temperature. The degree of freedom of gas molecule is
View Solution
Knowledge Check
For adiabatic process of an ideal gas the value of dPP is equals to
A−γdVVB−γVdVCdVVD−γ2dVVThe isothermal Bulk modulus of an ideal gas at pressure P is
APBλpCp/2DP/λIn an adiabatic process, R=23Cv. The pressure of the gas will be proportional to:
AT5/3BT5/2CT5/4DT5/6
The adiabatic Bulk modulus of a perfect gas at pressure is given by
View SolutionAssertion A diabatic bulk modulus of an ideal gas in more than its isothermal bulk modulus.
Reason Both the modulii aer proportional to the pressure of gas at that moment.
View SolutionChoose the most appropriate option.
During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio of CpCv for the gas is
View SolutionThe adiabatic Bulk modulus of a diatomic gas at atmosheric pressure is
View SolutionValue of adiabatic bulk modulus of elasticity of helium at NTP is
View Solution
