If two tangents inclined at an angle of 60∘ are drawn to a circle of radius 4 cm, then the length of each tangent is equal to :
2√3 cm
8 cm
4 cm
4√3 cm
The correct Answer is:D
To solve the problem of finding the length of each tangent drawn to a circle of radius 4 cm, inclined at an angle of 60 degrees, we can follow these steps:
1. Understand the Geometry:
- We have a circle with center O and radius 4 cm.
- Two tangents are drawn from a point P outside the circle, forming an angle of 60 degrees between them.
2. Identify the Angles:
- The angle between the two tangents (∠APB) is given as 60 degrees.
- Since the tangents are equal in length, we can bisect this angle. Thus, each angle (∠OAP and ∠OBP) will be half of 60 degrees, which is 30 degrees.
3. Use the Right Triangle:
- In triangle OAP, where OA is the radius (4 cm) and AP is the tangent we want to find, we know that ∠OAP = 30 degrees.
- The relationship between the sides of the triangle can be expressed using the tangent function:
tan(30∘)=OAAP
4. Substituting Known Values:
- We know that tan(30∘)=1√3.
- Substituting the known values into the equation gives:
1√3=4AP
5. Solving for AP:
- Rearranging the equation to find AP:
AP=4⋅√3
6. Final Answer:
- Therefore, the length of each tangent is:
AP=4√3 cm
Summary:
The length of each tangent drawn to the circle is 4√3 cm.
- We have a circle with center O and radius 4 cm.
- Two tangents are drawn from a point P outside the circle, forming an angle of 60 degrees between them.
- The angle between the two tangents (∠APB) is given as 60 degrees.
- Since the tangents are equal in length, we can bisect this angle. Thus, each angle (∠OAP and ∠OBP) will be half of 60 degrees, which is 30 degrees.
- In triangle OAP, where OA is the radius (4 cm) and AP is the tangent we want to find, we know that ∠OAP = 30 degrees.
- The relationship between the sides of the triangle can be expressed using the tangent function:
tan(30∘)=OAAP
- We know that tan(30∘)=1√3.
- Substituting the known values into the equation gives:
1√3=4AP
- Rearranging the equation to find AP:
AP=4⋅√3
- Therefore, the length of each tangent is:
AP=4√3 cm
The length of each tangent drawn to the circle is 4√3 cm.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - UNIT TEST - 425videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - QUESTION BANK - 431videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET10videos
AVERAGE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Self Assessment Sheet10videos
CO-ORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
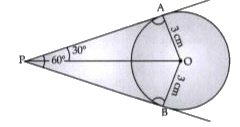
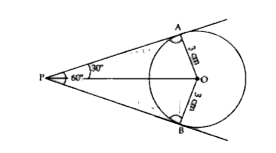
IF two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to
A3√32 cmB6 cmC3 cmD3√3cm - Question 2 - Select One
If two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3cm then the length of each tangent is
A3cmB3√32cmC3√3cmD6cm
If two tangents inclinced at an angle 60∘ are drawn to a circle of radius 3 cm, then find the length of each tangent.
View SolutionIf two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then what is the length of each tangent ?
View SolutionIf two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.View SolutionTwo tangents making an angle of 1200 with each other are drawn to a circle of radius 6cm, then the length of each tangent is equal to √3 cm (b) 6 √3 cm (c) √2 cm (d) 2 √3 cm
View SolutionTwo tangents making an angle of 60∘ between them, are drawn to a circle of radius √2 cm, then find the length of each tangent.
View SolutionIn figure ,PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm .If Pa⊥PB ,then the length of each tangent is :
 View Solution
View Solution