Two tangents making an angle of 60∘ between them, are drawn to a circle of radius √2 cm, then find the length of each tangent.
The correct Answer is:3 cm
To find the length of each tangent drawn to a circle of radius √2 cm, making an angle of 60∘ between them, we can follow these steps:
1. Understand the Geometry:
- Let C be the center of the circle, and A be the point where the tangents touch the circle. The points where the tangents touch the circle can be denoted as B and D. The angle between the two tangents AB and AD is given as 60∘.
2. Bisect the Angle:
- Since the tangents AB and AD meet at point A and form an angle of 60∘, the angle between the radius CB (or CD) and the tangent AB (or AD) is 90∘. Therefore, the angle CAB is half of 60∘, which is 30∘.
3. Use Right Triangle Properties:
- In triangle CBA, we have:
- CB=radius=√2 cm
- ∠CAB=30∘
4. Apply the Tangent Function:
- Using the tangent function in triangle CBA:
tan(30∘)=BCAB
- We know that tan(30∘)=1√3.
5. Set Up the Equation:
- Substitute the known values into the equation:
1√3=√2AB
6. Solve for AB:
- Rearranging the equation gives:
AB=√2⋅√3=√6 cm
7. Conclusion:
- Therefore, the length of each tangent AB and AD is √6 cm.
Final Answer:
The length of each tangent is √6 cm.
- Let C be the center of the circle, and A be the point where the tangents touch the circle. The points where the tangents touch the circle can be denoted as B and D. The angle between the two tangents AB and AD is given as 60∘.
- Since the tangents AB and AD meet at point A and form an angle of 60∘, the angle between the radius CB (or CD) and the tangent AB (or AD) is 90∘. Therefore, the angle CAB is half of 60∘, which is 30∘.
- In triangle CBA, we have:
- CB=radius=√2 cm
- ∠CAB=30∘
- Using the tangent function in triangle CBA:
tan(30∘)=BCAB
- We know that tan(30∘)=1√3.
- Substitute the known values into the equation:
1√3=√2AB
- Rearranging the equation gives:
AB=√2⋅√3=√6 cm
- Therefore, the length of each tangent AB and AD is √6 cm.
The length of each tangent is √6 cm.
Topper's Solved these Questions
- PRACTICE PAPER IIBook:CBSE COMPLEMENTARY MATERIALChapter:PRACTICE PAPER IIExercise:SECTION B
Explore 7 Videos
- PRACTICE PAPER IIBook:CBSE COMPLEMENTARY MATERIALChapter:PRACTICE PAPER IIExercise:SECTION C
Explore 14 Videos
- POLYNOMIALSBook:CBSE COMPLEMENTARY MATERIALChapter:POLYNOMIALSExercise:Practice test
Explore 10 Videos
- PRACTICE PAPER- I (WITH SOLUTIONS) CLASS: X Mathematics (Standard)Book:CBSE COMPLEMENTARY MATERIALChapter:PRACTICE PAPER- I (WITH SOLUTIONS) CLASS: X Mathematics (Standard)Exercise:SECTION -D
Explore 6 Videos
Similar Questions
Two tangents making an angle of 1200 with each other are drawn to a circle of radius 6cm, then the length of each tangent is equal to √3 cm (b) 6 √3 cm (c) √2 cm (d) 2 √3 cm
View SolutionIf two tangents inclinced at an angle 60∘ are drawn to a circle of radius 3 cm, then find the length of each tangent.
View Solution
Knowledge Check
IF two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to
A3√32 cmB6 cmC3 cmD3√3cmIf two tangents inclined at an angle of 60∘ are drawn to a circle of radius 4 cm, then the length of each tangent is equal to :
A2√3 cmB8 cmC4 cmD4√3 cmIf two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3cm then the length of each tangent is
A3cmB3√32cmC3√3cmD6cm
If two tangents inlined at an angle 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to :
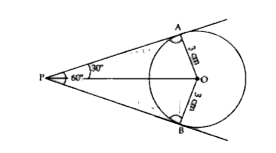
View SolutionIf two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then what is the length of each tangent ?
View SolutionIf two tangents inclined at an angle 60∘ are drawn to a circle of radius 3 cm, then, the length of each tangent is equal to
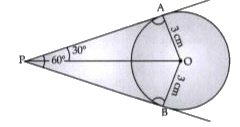
View SolutionIf two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.
View SolutionFind the distance between two parallel tangents of a circle of radius 3 cm.
View Solution