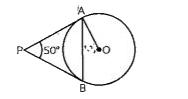
In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
36∘
18∘
27∘
36∘
The correct Answer is:C
To solve for the angle OAB given that PA and PB are tangents to the circle with center O and that angle APB is 54 degrees, we can follow these steps:
1. Identify the Given Information:
- PA and PB are tangents to the circle.
- Angle APB = 54 degrees.
2. Use the Property of Tangents:
- The lengths of tangents drawn from an external point to a circle are equal. Therefore, PA = PB.
3. Set Up the Angles:
- Let angle OAP = angle OBP = α (since PA = PB, the angles opposite to equal sides are equal).
4. Apply the Triangle Angle Sum Property:
- In triangle APB, the sum of angles is 180 degrees.
- Therefore, we can write:
∠OAP+∠OBP+∠APB=180∘
- Substituting the known values:
α+α+54∘=180∘
- This simplifies to:
2α+54∘=180∘
5. Solve for α:
- Rearranging gives:
2α=180∘−54∘
2α=126∘
α=126∘2=63∘
6. Use the Tangent-Radius Property:
- The tangent at point A and the radius OA form a right angle:
∠OAP+∠OAB=90∘
- Substituting α for angle OAP:
63∘+∠OAB=90∘
7. Solve for Angle OAB:
- Rearranging gives:
∠OAB=90∘−63∘=27∘
Final Answer:
- Therefore, angle OAB = 27 degrees.
---
- PA and PB are tangents to the circle.
- Angle APB = 54 degrees.
- The lengths of tangents drawn from an external point to a circle are equal. Therefore, PA = PB.
- Let angle OAP = angle OBP = α (since PA = PB, the angles opposite to equal sides are equal).
- In triangle APB, the sum of angles is 180 degrees.
- Therefore, we can write:
∠OAP+∠OBP+∠APB=180∘
- Substituting the known values:
α+α+54∘=180∘
- This simplifies to:
2α+54∘=180∘
- Rearranging gives:
2α=180∘−54∘
2α=126∘
α=126∘2=63∘
- The tangent at point A and the radius OA form a right angle:
∠OAP+∠OAB=90∘
- Substituting α for angle OAP:
63∘+∠OAB=90∘
- Rearranging gives:
∠OAB=90∘−63∘=27∘
- Therefore, angle OAB = 27 degrees.
Topper's Solved these Questions
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:UNIT TEST - 4
Explore 25 Videos
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:QUESTION BANK - 43
Explore 1 Video
- AVERAGEBook:S CHAND IIT JEE FOUNDATIONChapter:AVERAGEExercise:SELF ASSESSMENT SHEET
Explore 10 Videos
- CO-ORDINATE GEOMETRYBook:S CHAND IIT JEE FOUNDATIONChapter:CO-ORDINATE GEOMETRYExercise:Self Assessment Sheet
Explore 10 Videos
Similar Questions
Knowledge Check
If PA and PB are tangents to the circle with centre O such that ∠APB=50∘ then ∠OAB is equal to
A50∘B30∘C40∘D25∘In figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
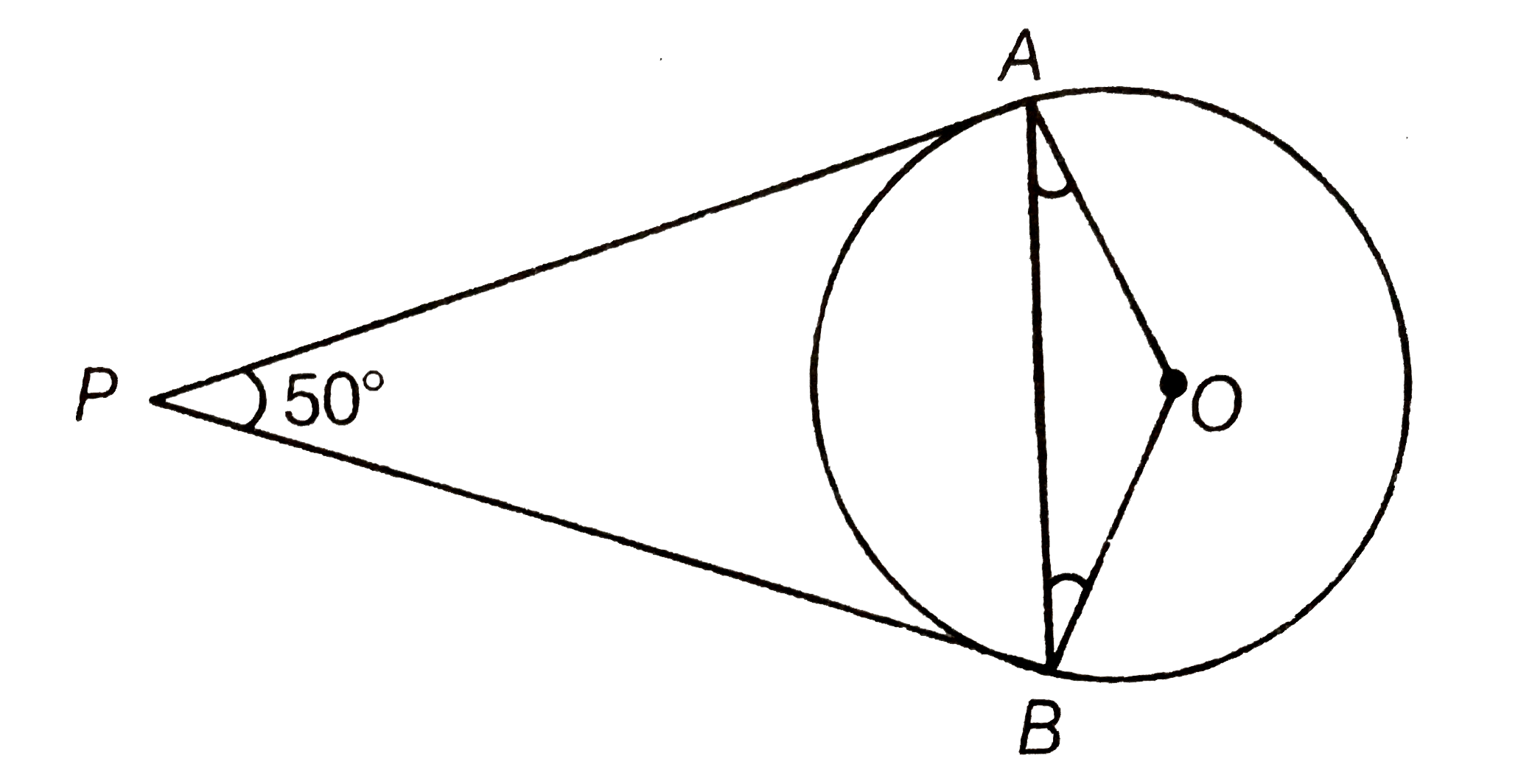 A25∘B30∘C40∘D50∘
A25∘B30∘C40∘D50∘If PA and PB are two tangents to a circle with centre O such that ∠APB=80∘, then, ∠AOP=?
A40∘B50∘C60∘D70∘
In the given figure, PA and PB are tangents to a circle with centre O. Prove that ∠APB and ∠AOB are supplementary.

View SolutionPA and PB are the tangent on a circle with centre O such that ∠APB=42∘. What will be the value of ∠AOB?
View SolutionIn the given figure, AP and BP are tangents to a circle with centre O. IF ∠APB=62∘ then the measure of ∠AQB is

View SolutionIn the given figure, AB and AC are tangents to the circle with centre O. Given that ∠BAC=70∘ and P is a point on the minor are BC, find ∠ BPC.
View SolutionIn the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
View Solution