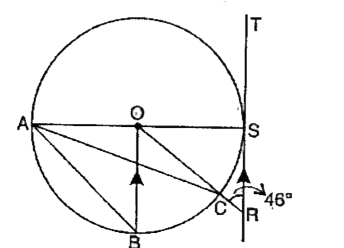
In the given figure, RST is the tangent to the circle with centre O, at S. AOS is a straight line BO||RT and ∠ORS=46∘. Then ∠ BAC equals
A
22∘
B
46∘
C
23∘
D
32∘
Video Solution
Text Solution
The correct Answer is:C
|
Answer
Step by step video, text & image solution for In the given figure, RST is the tangent to the circle with centre O, at S. AOS is a straight line BO||RT and angle ORS = 46^(@). Then angle BAC equals by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:UNIT TEST - 4
Explore 25 Videos
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:QUESTION BANK - 43
Explore 1 Video
- AVERAGEBook:S CHAND IIT JEE FOUNDATIONChapter:AVERAGEExercise:SELF ASSESSMENT SHEET
Explore 10 Videos
- CO-ORDINATE GEOMETRYBook:S CHAND IIT JEE FOUNDATIONChapter:CO-ORDINATE GEOMETRYExercise:Self Assessment Sheet
Explore 10 Videos
Similar Questions
Knowledge Check
In the diagram, CB and CD are tangents to the circle with centre O. AOC is a straight line and ∠OCB=34∘.∠ABO equals.
 A56∘B28∘C34∘D32∘
A56∘B28∘C34∘D32∘In the given figure, O is the centre of the circle. Then ∠AED measure
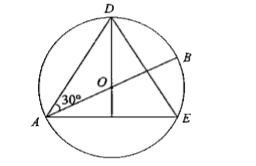 A30∘B45∘C60∘D90∘
A30∘B45∘C60∘D90∘In the given figure, O is the centre of the circle. The measure of ∠ ADB is
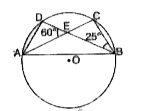 A90∘B85∘C95∘D120∘
A90∘B85∘C95∘D120∘
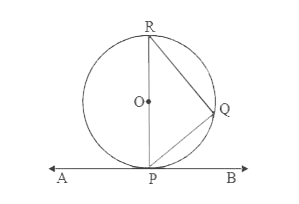
In Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
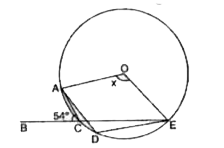
View SolutionIn the given figure, O is the centre of the circle, ∠ACB=54∘ and BCF is a straight line. Find x.
View SolutionO is the centre of the circle, ABN is a straight line. Find ∠AOC.

View SolutionIn the given figure (if O is the centre of circle.) , ∠COE measure
View Solution