In an isoceles triangle OAB , O is the origin and OA=OB=6 . The equation of the side AB is x-y+1=0 Then the area of the triangle isSolution in Bengali
2√21
√142
√1422
√712
The correct Answer is:D
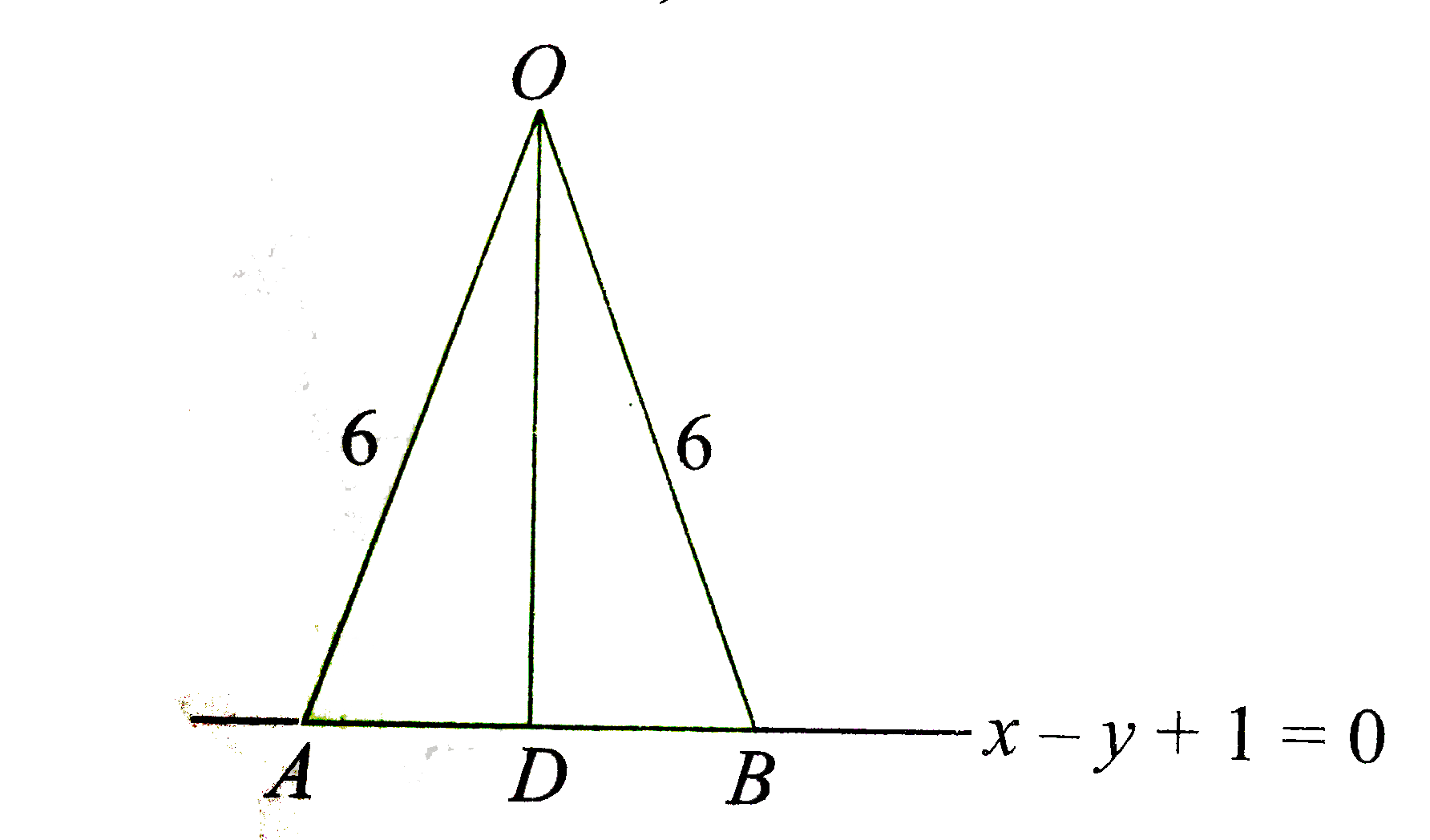
Let D be the midpoint of AB.
OD=1√2
AD=√62−OD2=√36−12=√172
∴Area of triangle=12×AB×OD=√172×√12=√712
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionIn an isoceles triangle OAB,O is the origin and OA=OB=6 .The equation of the side AB is x-y+1=0 Then the area of the triangle is
View Solutiono is the origin. A and B are variable points on y =x and x +y=0 such that the area of triangle OAB is k^2. The locus of the circumcentre of triangle OAB is
View SolutionLety=x line is median of the triangle OAB where O is origin. Equation ax2+2hxy+by2=0,a,h,b∈N, represents combined equation of OA and OB. A and B lie on the ordinate x=3. If slope of OA is twice the slope of OB, then greatest possible value of a+2h+b is
View SolutionA variable line cuts X-axis at A, Y -axix at B, where OA = a, OB = b (O as origin) such that a2+b2=1.
Find the locus of
centroid of ΔOAB
View SolutionThe line x + y = p meets the axis of x and y at A and B respectively. A triangle APQ is inscribed in the triangle OAB, O being the origin, with right angle at Q, P and Q lie respectively on OB and AB. If the area of the triangle APQ is 3/8th of the area of the triangle OAB, then AQBQ is equal to
View SolutionThe line x+y=a meets the axes of x and y at A and B respectively. A triangle AMN is inscribed in the triangle OAB, O being the origin, with right angle at N, M and N lie respectively on OB and AB. If the area of the triangle AMN is 38 of the area of the triangle OAB, then ANBM is equal to:
View SolutionIf O is the origin and A and B are points on the line 3x−4y+25=0 such that OA=OB=13, Then the area of ΔOAB (In sq units) is
View SolutionIn an isoceles triangle OAB , O is the origin and OA=OB=6 . The equation of the side AB is x-y+1=0 Then the area of the triangle is
View SolutionLety=x line is median of the triangle OAB where O is origin. Equation ax2+2hxy+by2=0,a,h,b∈N, represents combined equation of OA and OB. A and B lie on the ordinate x=3. If slope of OA is twice the slope of OB, then greatest possible value of a+2h+b is
View SolutionThe line x + y = p, x and y axis meet at A and B respectively. A triangle APQ that is right-angled at Q is under the triangle OAB, where 0 is the origin. P and Q are located at OB and AB respectively. If the area of triangle APQ is 3/8 of the area of triangle OAB, then (AQ)/(BQ) Is equal -
View SolutionIn the isosceles triangle OAB, O is the origin, OA=OB=6. If the equation of side AB is x−y+1=0, then the area of the triangle OAB is (in square units)
View Solution
