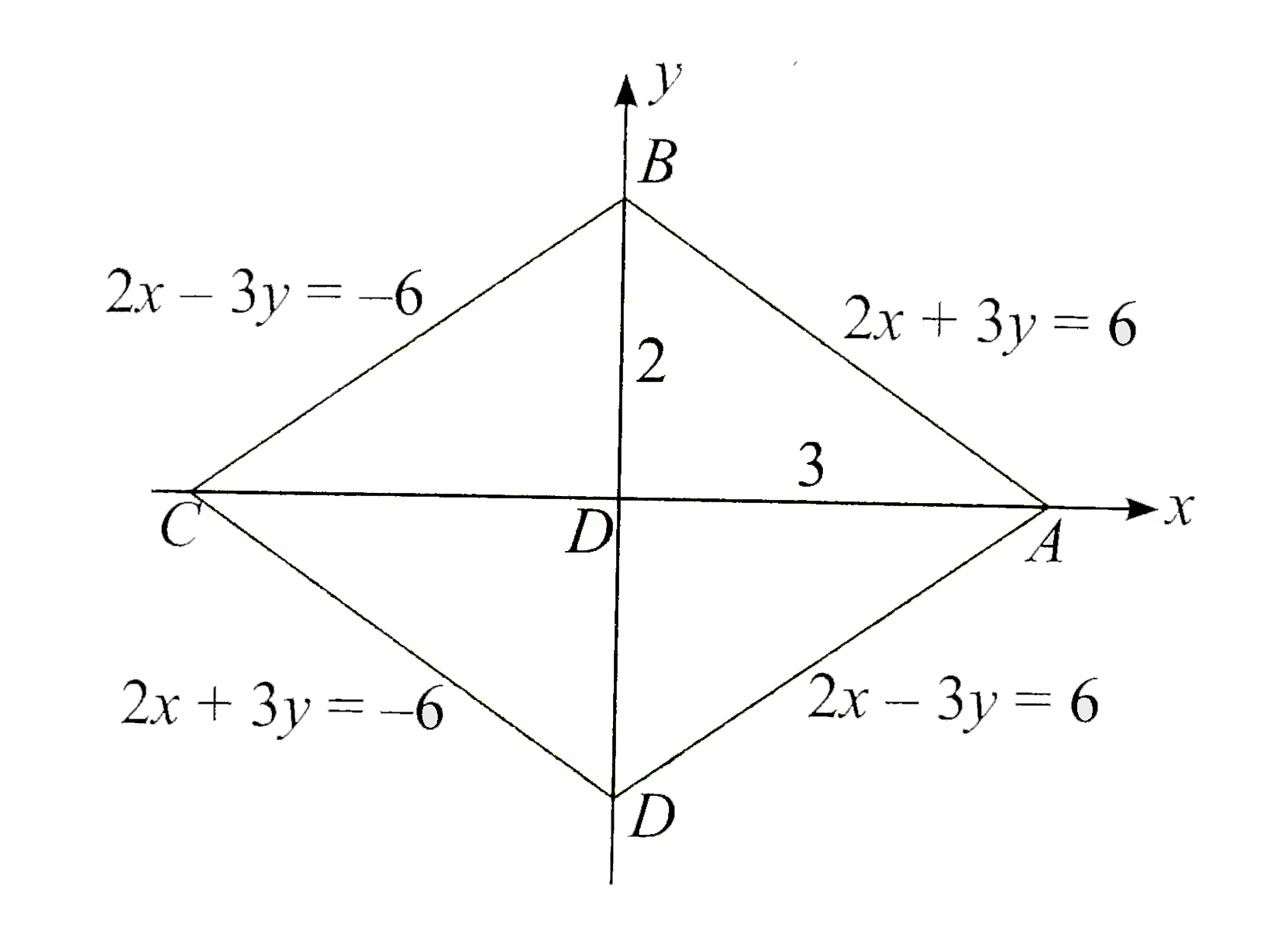
The area enclosed by 2|x|+3|y|≤6 is (a) 3 sq. units (b) 4 sq. units 12 sq. units (d) 24 sq. unitsSolution in Bengali
3 sq. units
4 sq. units
12 sq. units
24 sq. units
The correct Answer is:C
The given inequality is equivalent to the following system of inequalities.
2x+3y≤6,when x≥0,y≥0
2x−3y≤6,when x≥0,y≤0
−2x+3y≤6,when x≤0,y≥0
−2x−3y≤6,when x≤0,y≤0
which represents a rhombus with sides
2x±3y=6 and 2x±3y=−6
The lengths of the diagonals are 6 units and 4 units, respectively, along the x- and y-axes. Therefore, the required area is 1/2×6×4=12 sq. units.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionThe area bounded by the loop of the curve 4y2=x2(4−x2) is 7/3 sq. units (b) 83sq.unites 113sq.units (d) 163sq.units
View SolutionThe area bounded by the parabola y=(x+1)2 and y=(x−1)2 and the line y=14 is (A) 4 sq. units (B) 16 sq. units (C) 34 sq. units (D) 13 sq. units
View SolutionThe area bounded by the curve y=4x−x2 and x-axis is (A) 307 sq. units (B) 317 sq. units (C) 323 sq. units (D) 343 sq. units
View SolutionThe area of the region bounded by the curves y=|x−1| and y=3−|x| is (A) 6 sq. units (B) 2 sq. units (C) 3 sq. units (D) 4 sq. units
View SolutionThe area bounded by the curves y=logex and y=(logex)2 is (A) e−2 sq. units (B) 3−e sq. units (C) e sq. units (D) e−1 sq. units
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
View SolutionThe area bounded by the parabolas y=(x+1)2 and y=(x−1)2andy=(x−1)2 and the line y=14 is 4 sq. units (b) 1/6 sq. units 4/3 sq. units (d) 1/3 sq. units
View SolutionThe area enclosed by 2|x|+3|y|≤6 is (a)3 sq. units (b) 4 sq. units (c)12 sq. units (d) 24 sq. units
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
View SolutionThe area of the triangle formed by the line x=3, y=4 and x=y is (a)12sq.unit (b)1sq.unit (c)2sq.unit (d) None of these
View SolutionThe area bounded by the curve y=4x−x2 and x-axis is (A) 307 sq. units (B) 317 sq. units (C) 323 sq. units (D) 343 sq. units
View Solution
