If a pair of perpendicular straight lines drawn through the origin forms an isosceles triangle with the line $2 x + 3 y = 6$ , then area of the triangle so formed is Solution in Bengali

A

$\frac{36}{13} sq. unit$

B

$\frac{12}{17} sq. unit$

C

$\frac{13}{5} sq. unit$

D

$\frac{17}{13} sq. unit$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

As shown in the following figure, pair of perpendicular lines through origin meets given line 2x+3y=6 at A and B such that AOB is right angled isosceles triangle.

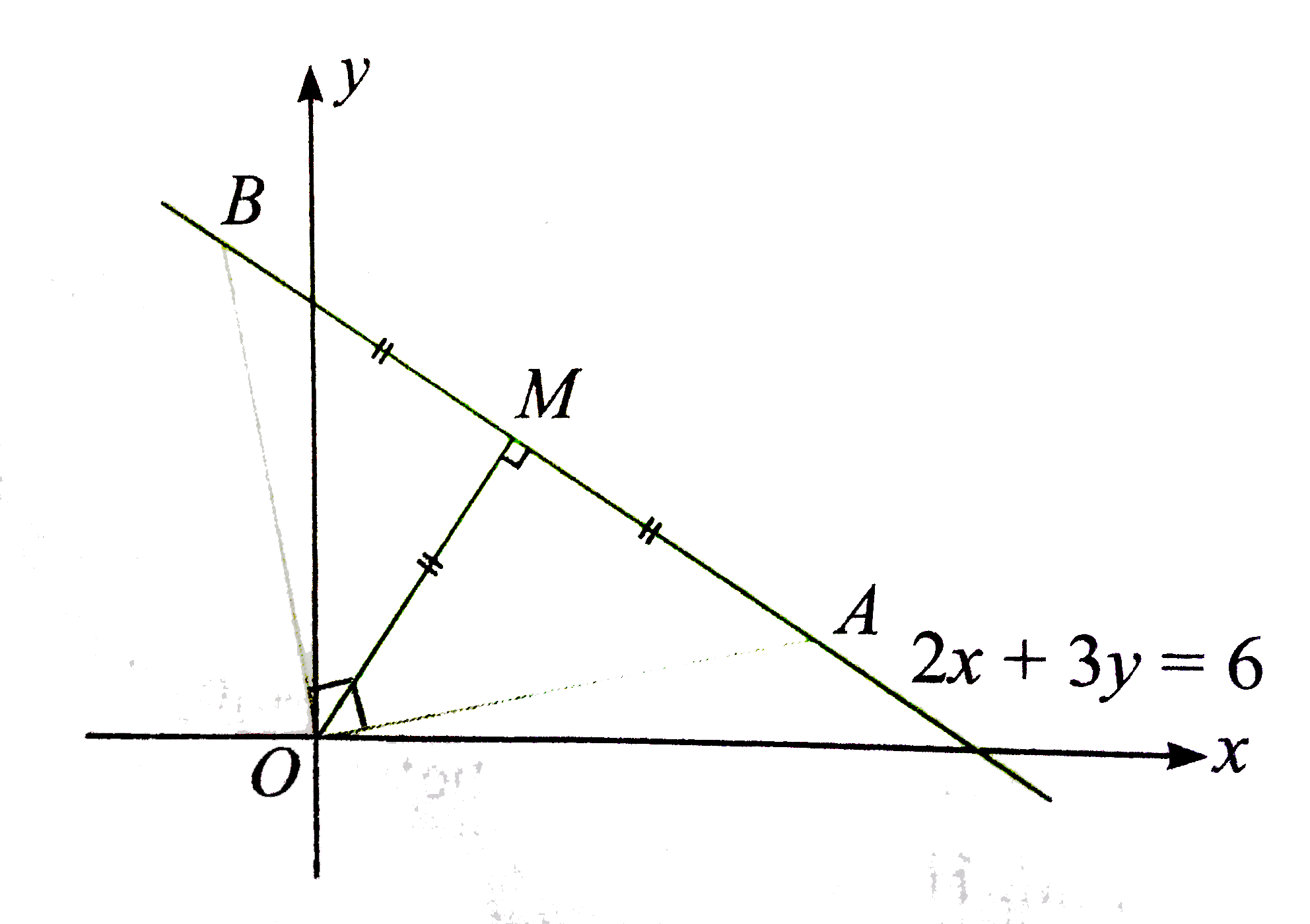
Now, OM=BM=AM, where OM $= \frac{| 0 + 0 - 6 |}{\sqrt{2^{2} + 3^{2}}} = \frac{6}{\sqrt{13}}$
$∴ A B = 2 A M = 2 O M = \frac{12}{\sqrt{13}}$
$∴ Area of triangle A O B = \frac{1}{2} \times \frac{12}{\sqrt{13}} \times \frac{6}{\sqrt{13}} = \frac{36}{13}$ sq. units.

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-STRAIGHT LINES-EXERCISE (SINGLE CORRECT ANSWER TYPE)

Home
Ask Doubt
Profile