In an isoceles triangle OAB , O is the origin and OA=OB=6 . The equation of the side AB is x-y+1=0 Then the area of the triangle is
2√21
√142
√1422
√712
The correct Answer is:D
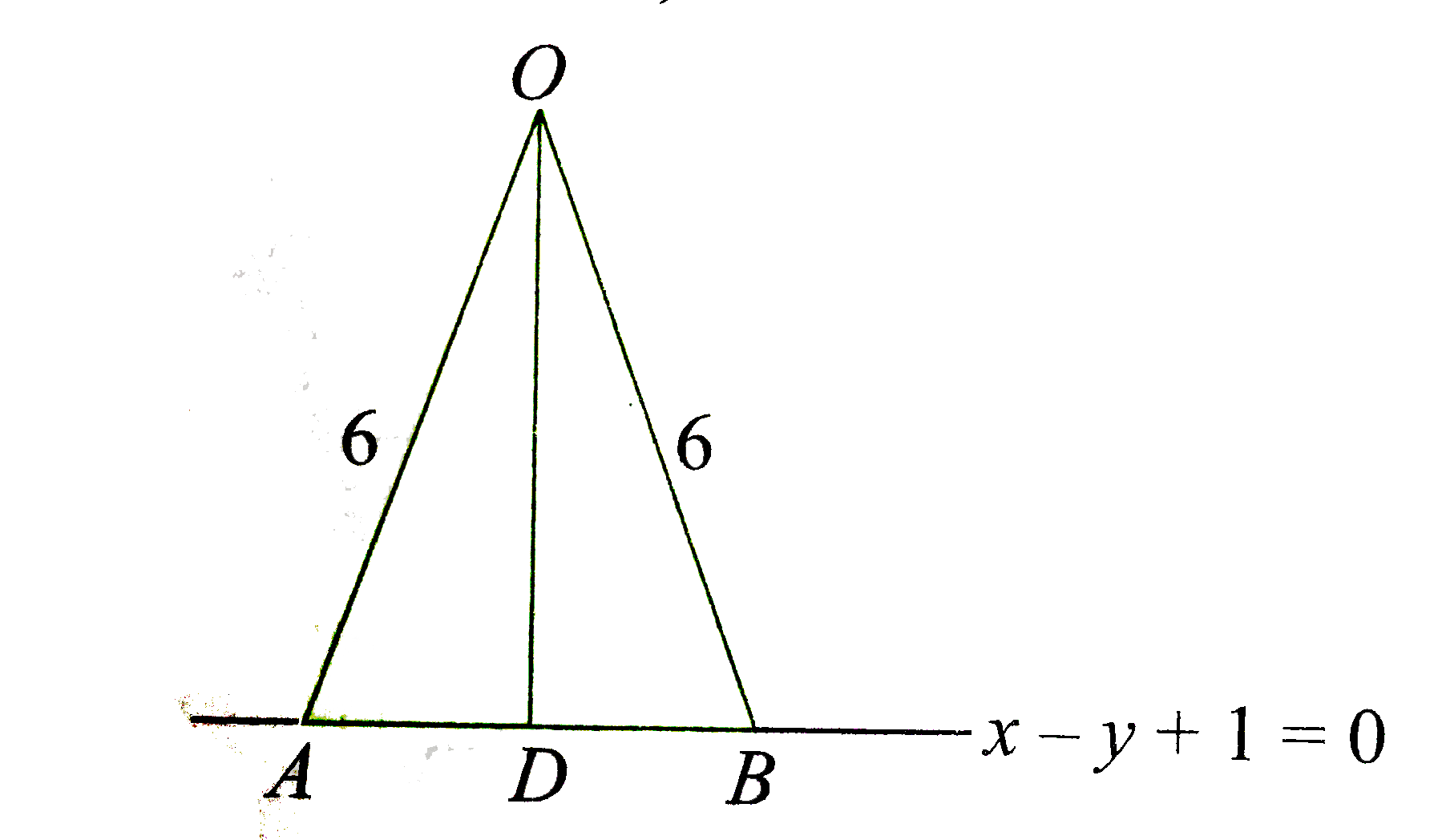
Let D be the midpoint of AB.
OD=1√2
AD=√62−OD2=√36−12=√172
∴Area of triangle=12×AB×OD=√172×√12=√712
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
If the ends of the base of an isosceles triangle are at (2, 0) and (0, 1), and the equation of one side is x=2, then the orthocenter of the triangle is
View SolutionIf a vertex of an equilateral triangle is the origin and the side opposite to it has the equation x+y=1, then orthocentre of the triangle is :
View SolutionLet ΔABC is an isosceles trianlge with AB=AC. If B=(0,a),C=(2a,0) and the equation of AB is 3x−4y+4a=0, then the equation of side AC is
View SolutionIn triangle ABC , the equation of side BC is x−y=0. The circumcenter and orthocentre of triangle are (2, 3) and (5, 8), respectively. The equation of the circumcirle of the triangle is a) x2+y2−4x+6y−27=0 b) x2+y2−4x−6y−27=0 c) x2+y2+4x−6y−27=0 d) x2+y2+4x+6y−27=0
View SolutionThe equation of the sides of a triangle are x+2y+1=0,2x+y+2=0andpx+qy+1=0 and area of triangle is Δ .
View SolutionIf a plane cuts off intercepts OA=a,OB=b,OC=c from the coordinate axes 9where 'O' is the origin). then the area of the triangle ABC is equal to
View SolutionLet O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
View SolutionIf the point 3x+4y−24=0 intersects the X-axis at the point A and the Y-axis at the point B, then the incentre of the triangle OAB, where O is the origin, is
View SolutionLet A(2,0) and B(z) are two points on the circle |z|=2. M(z') is the point on AB. If the point ¯z' lies on the median of the triangle OAB where O is origin, then arg(z') is
View SolutionThe co-ordinates of the vertex of an equilateral triangle are (2,−1) and equation of its base is x+y−1=0. Find the equations of its other two sides.
View Solution
