A line of fixed length 2 units moves so that its ends are on the positive x-axis and that part of the line $x + y = 0$ which lies in the second quadrant. Then the locus of the midpoint of the line has equation.

A

$x^{2} + 5 y^{2} + 4 x y - 1 = 0$

B

$x^{2} + 5 y^{2} + 4 x y + 1 = 0$

C

$x^{2} + 5 y^{2} - 4 x y - 1 = 0$

D

$x^{2} + 5 y^{2} - 4 x y - 1 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

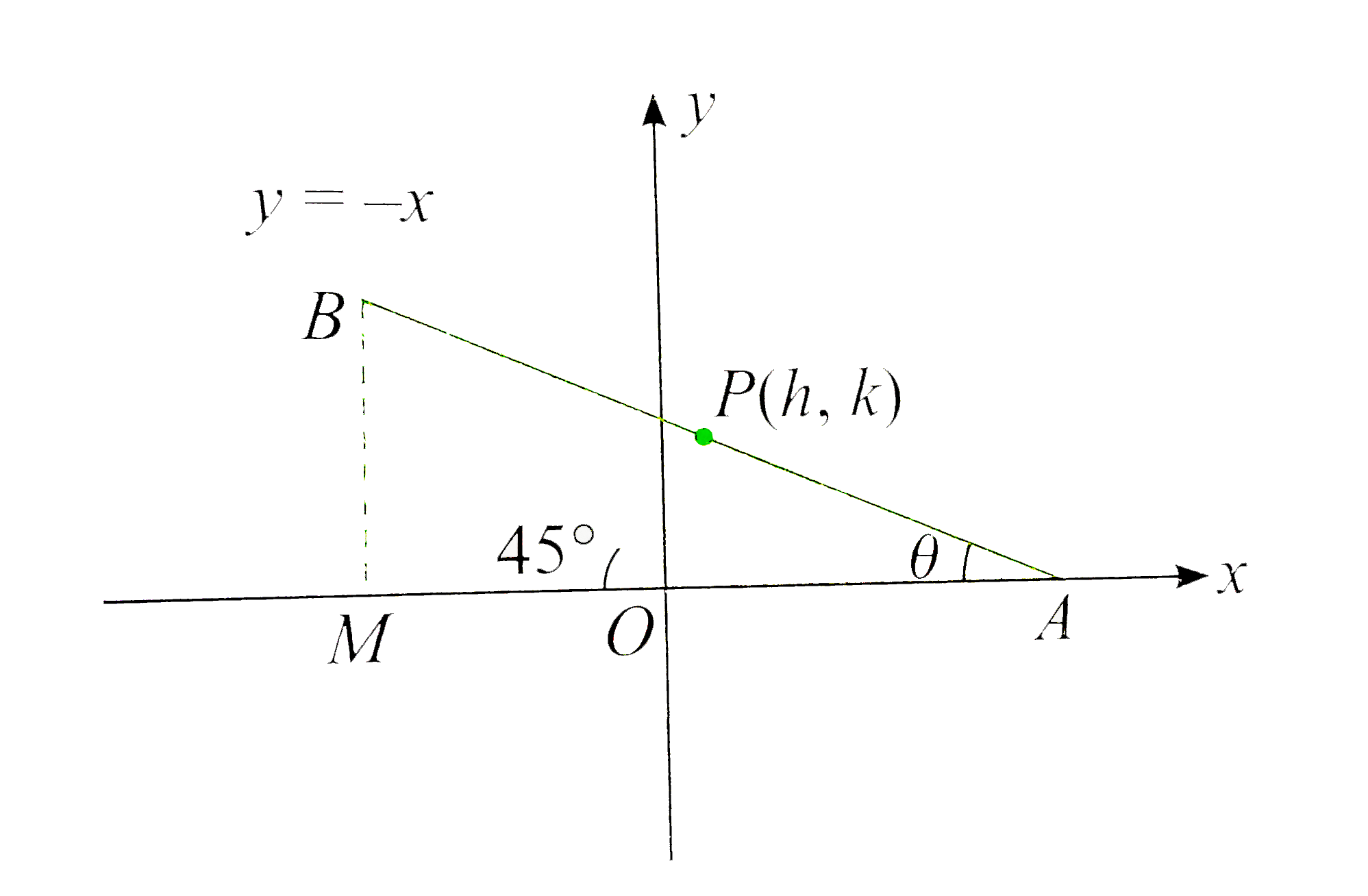
As shown in the figure, line segment AB, of fixed length 2 units, slides such that one of its ends A is on x-axis and other end B is on line x+y=0.
Let P(h,k) be midpoint of AB.
Also, let $∠ B A O = θ$ .
So, in triangle AMB, BM = $2 sin θ and A M = 2 cos θ .$
In triangle BMO, MO=MB = $2 sin θ$
$∴ A \equiv (2 cos θ - 2 sin θ, 0) and B \equiv (- 2 sin θ, 2 sin θ)$
Now, P(h,k) is the midpoint of AB.
$∴ 2 h = 2 cos θ - 2 sin θ + (- 2 sin θ) and 2 k = 2 sin θ$
$\Rightarrow h = cos θ - 2 sin θ and k = sin θ$
$\Rightarrow h + 2 k = cos θ and k = sin θ$
Squaring and adding, we get
${(h + 2 k)}^{2} + k^{2} = 1$
$or x^{2} + 5 y^{2} + 4 x y - 1 = 0$
This is the required locus.

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-STRAIGHT LINES-EXERCISE (SINGLE CORRECT ANSWER TYPE)

Home
Ask Doubt
Profile