Question

$A\equiv (-4,0),B\equiv (4,0)\stackrel{.}{M}andN$
are the variable
points of the y-axis such that $M$
lies below $NandMN=4$
. Lines $AMandBN$
intersect at $P\stackrel{.}{}$
The locus of $P$
is
(a) $2xy-16-x^2=0$

(b) $2xy+16-x^2=0$

(c) $2xy+16+x^2=0$

(d) $2xy-16+x^2=0$

Options

A. `2xy-16-x^(2) = 0`
B. `2xy+16-x^(2) = 0`
C. `2xy+16+x^(2) = 0`
D. `2xy-16+x^(2) = 0`

Answer

D

Explanation

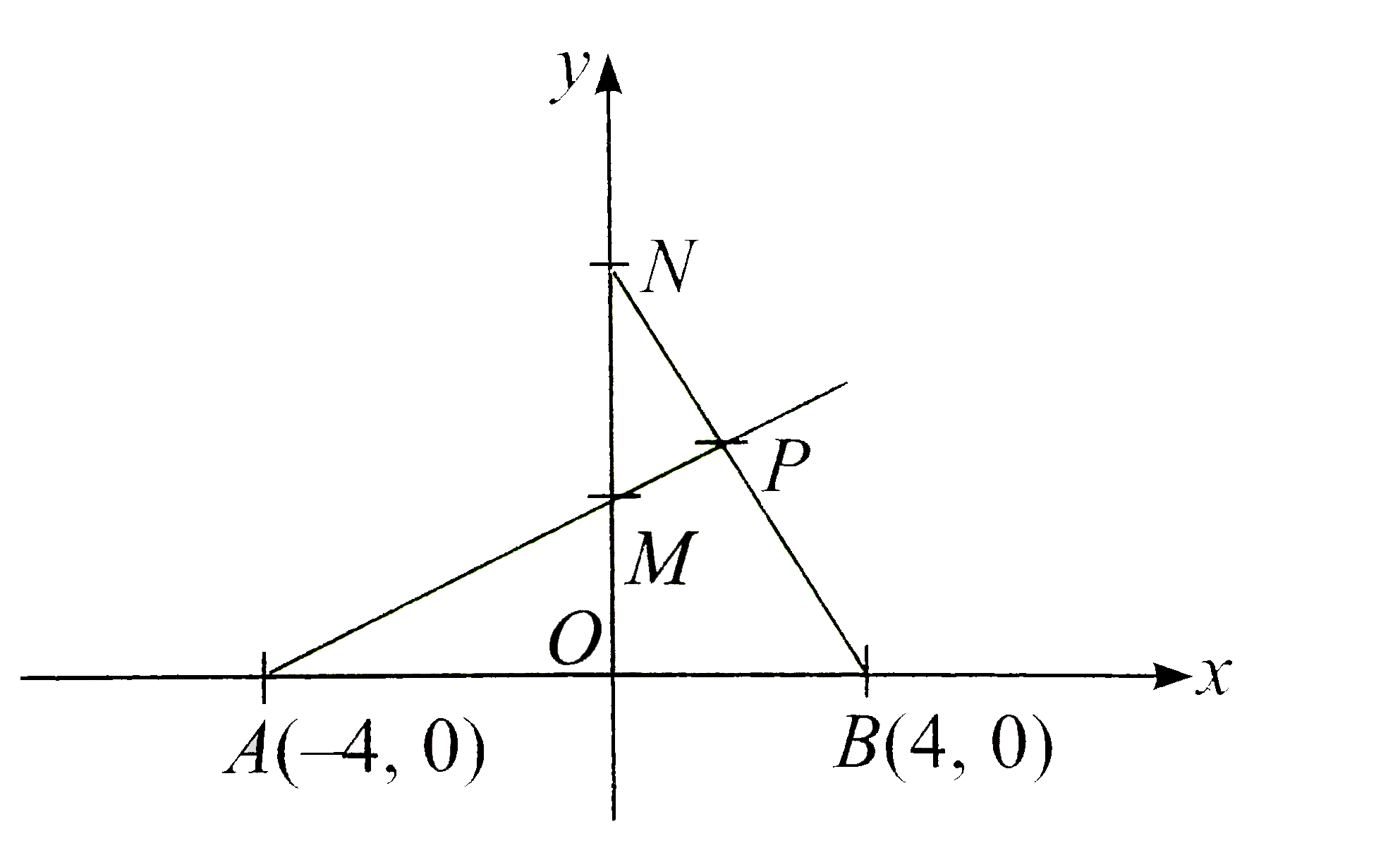
`"Let "M-=(0,h). "Then"`
`"or " N-=(0,h+4)`
The equation of AM is
`(x)/(-4) + (y)/(h) = 1`
`"or " (y)/(h) = (4+x)/(4)`
`"or " h = (4y)/(4+x)`
The equation of BN is
`(x)/(4) + (y)/(h+4) = 1`
`"or " (y)/(h+4) = (4-x)/(4)`
`"or " h+4 = (4y)/(4-x)`
`"or " h= (4y-16+4x)/(4-x)`
`"or "(4(y-4+x))/(4-x) = (4y)/(4+x)` (Eliminating h)
`"or " 2xy-16+x^(2) = 0,` which is the required locus