The vertex A of ΔABC is (3,-1). The equation of median BE and angle bisector CF are x-4y+10=0 and 6x+10y-59=0, respectively. Equation of AC is
5x+18y=37
15x+8y=37
15x-8y=37
15x+8y+37=0
The correct Answer is:B
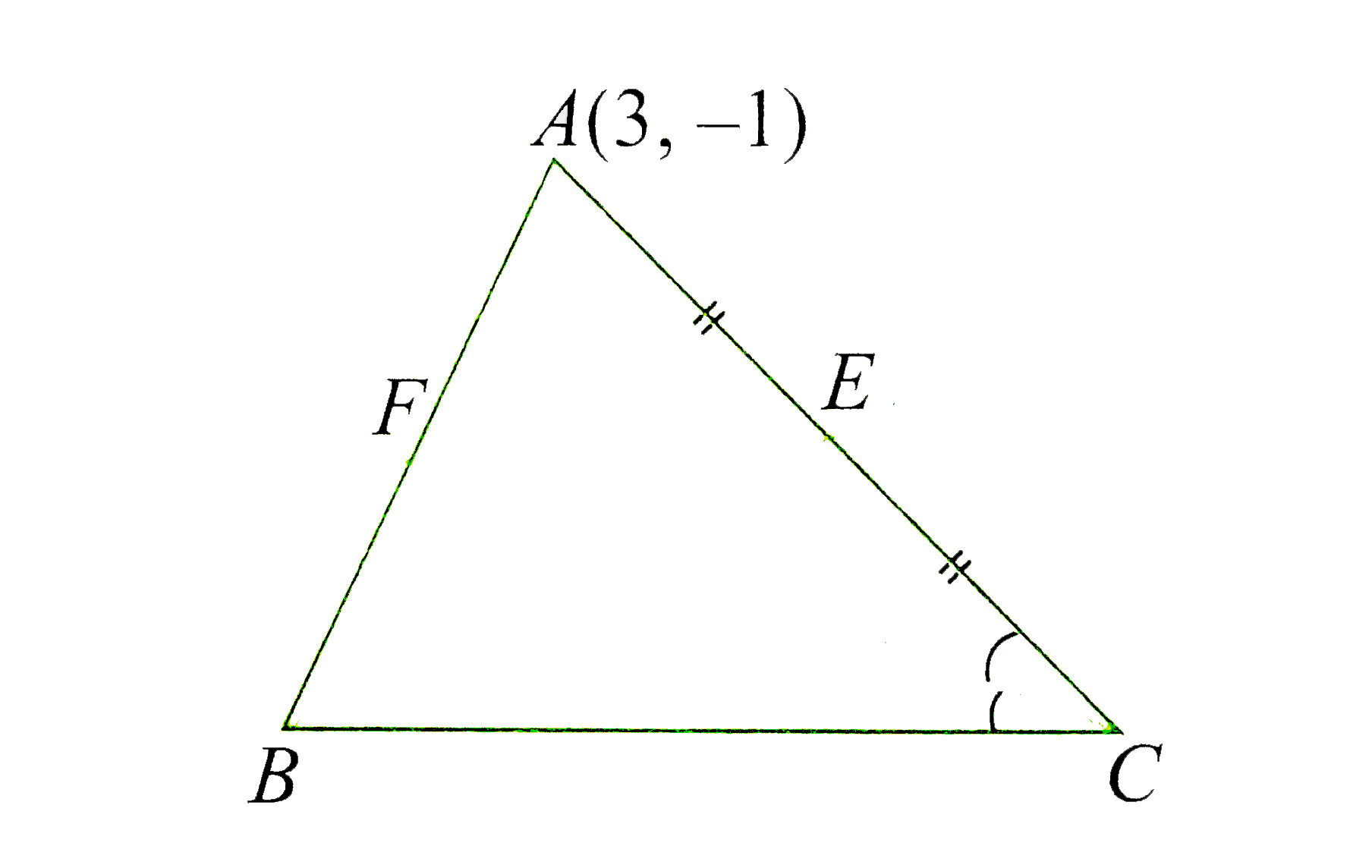
Point E is on the median x-4y+10=0.
∴E≡(x1,x1+104)
Point C is on the bisector 6x+10y-59=0.
∴C≡(x2,59−6x210)
Midpoint of AC is E.
∴x2+32=x1
⇒x2=2x1−3 (1)
and 59−6x210−12=x1+104
⇒49−6(2x1−3)20=x1+104
⇒49−12x1+18=5x1+50
⇒17x1=17
∴x1=1
Coordinates of E are (1,114).
Equation of AC is
(y+1)=114+1−2=(x−3)
⇒−8y−8=15x−45
⇒15x+8y=37
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Video
Similar Questions
Find the equation of acute angled bisector of lines :
3x−4y+7=0and12x−5y−8=0
View SolutionFind equation of angle bisector of plane x+2y+3z−z=0and2x−3y+z+4=0.
View SolutionLet A,B,C be angles of triangles with vertex A≡(4,−1) and internal angular bisectors of angles B and C be x−1=0 and x−y−1=0 respectively.
Slope of BC is
View SolutionIn a triangle ABC , if the equation of sides AB,BC and CA are 2x−y+4=0,x−2y−1=0andx+3y−3=0 respectively ,
The equation of external bisector of angle B is
View SolutionThe equation of the medians of a triangle formed by the lines x+y−6=0,x−3y−2=0 and 5x−3y+2=0 is
View SolutionFind the equation of the bisector of the acute angle between the lines 3x−4y+7=0and12x+5y−2=0.
View SolutionThe vertices of ΔABC are A(−3,2), B(0,3) and C(1,0). Find the equation of the median through B.
View SolutionLet the equations of side BC and the internal angle bisector of angle B of ΔABC are 2x−5y+a=0 and y+x=0 respectively. If A=(2,3), then the value of of a is equal to
View SolutionIn a triangle ABC , if the equation of sides AB,BC and CA are 2x−y+4=0,x−2y−1=0andx+3y−3=0 respectively ,Tangent of internal angle A
is equal to
View SolutionFind the equations of the sides of the triangle having (3,−1) as a vertex, x−4y+10=0and6x+10y−59=0 being the equations of an angle bisector and a median respectively drawn from different vertices.
View Solution
