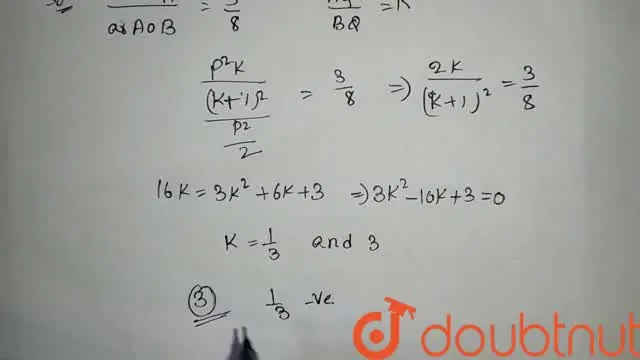The line x+y=p meets the x-and y-axes at A and B, respectively. A triangle APQ is inscribed in triangle OAB, O being with right at Q.P and Q lie, respectivley, on OB and AB. If the area of triangle APQ is th of the area of triangle OAB, then AQ/BQ is equal to Solution in Telugu
2
3
The correct Answer is:D
Step by step video, text & image solution for The line x+y=p meets the x-and y-axes at A and B, respectively. A triangle APQ is inscribed in triangle OAB, O being with right at Q.P and Q lie, respectivley, on OB and AB. If the area of triangle APQ is 3//8th of the area of triangle OAB, then AQ/BQ is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - PRACTICE SHEET(EXERCISE-I Problems on slopes, Equation of Lines and Interceptes of a line , Areas) (LEVEL -II More than One correct answer Type Questions)2videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - PRACTICE SHEET(EXERCISE-I Problems on slopes, Equation of Lines and Interceptes of a line , Areas(level-II)(Integer Type Question)3videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - LECTURE SHEET(EXERCISE-IV Problems on Anle between lines, Foot, Image Orthocentre, Circumcentre, Incentre, Angle Bisectors and Locus )(Integer Type Questions)4videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - REVISION EXERCISEEXERCISE - PROPERTIES OF TRIANGLES57videos
REVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - TANGENT AND NORMAL EXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS48videos
TANGENT AND NORMAL
Similar Questions
If the straight line ax+cy=2b, where a,b,c>0, makes a triangle of area 2 sq. units with the coordinate axes, then
05:38View SolutionThe area of the triangular region in the first quadrant bounded on the left by the y-axis, bounded above by the line 7x+4y=168, and bounded below by the line 5x+3y=121 is A. Then the value of 3A/10 is __________
15:13View SolutionP is the circumcenter of an equilateral triangle ABC of side lengh √3 units then the value of PA2+PB2+PC2 is
10:41View SolutionIn a triangle ABC, if A,B, C are in A.P and b:c =√3:√2, then
04:39View SolutionFind the equations of tangent and normal to the curve
(xa)4+(yb)4=2 at (a,b)09:41View SolutionThe line x+y=p meets the x- and y-axes at AandB , respectively. A triangle APQ is inscribed in triangle OAB,O being the origin, with right angle at Q.P and Q lie, respectively, on OBandAB . If the area of triangle APQ is 38th of the are of triangle OAB, the AQBQ is equal to (a)2(b) 23 (c) 13 (d)3
09:56View Solution(1)A triangle formed by the lines x+y=0 , x-y=0 and lx+my=1. If land m vary subject to the condition l^2+m^2=1 then the locus of the circumcentre of triangle is: (2)The line x +y= p meets the x-axis and y-axis at A and B, respectively. A triangle APQ is inscribed in triangle OAB, O being the origin, with right angle at Q. P and Q lie, respectively, on OB and AB. If the area of triangle APQ is 3/8th of the area of triangle OAB, then (AQ)/(BQ) is: equal to
02:02View SolutionIn an isoceles triangle OAB,O is the origin and OA=OB=6 .The equation of the side AB is x-y+1=0 Then the area of the triangle is
04:20View Solutiono is the origin. A and B are variable points on y =x and x +y=0 such that the area of triangle OAB is k^2. The locus of the circumcentre of triangle OAB is
10:46View SolutionThe line x + y = p meets the axis of x and y at A and B respectively. A triangle APQ is inscribed in the triangle OAB, O being the origin, with right angle at Q, P and Q lie respectively on OB and AB. If the area of the triangle APQ is 3/8th of the area of the triangle OAB, then AQBQ is equal to
04:21View SolutionThe line x+y=a meets the axes of x and y at A and B respectively. A triangle AMN is inscribed in the triangle OAB, O being the origin, with right angle at N, M and N lie respectively on OB and AB. If the area of the triangle AMN is 38 of the area of the triangle OAB, then ANBM is equal to:
View SolutionThe line x+y=p meets the x- and y-axes at AandB , respectively. A triangle APQ is inscribed in triangle OAB,O being the origin, with right angle at Q.P and Q lie, respectively, on OBandAB . If the area of triangle APQ is 38th of the are of triangle OAB, the AQBQ is equal to (a)2(b) 23 (c) 13 (d)3
05:38View SolutionIn an isoceles triangle OAB , O is the origin and OA=OB=6 . The equation of the side AB is x-y+1=0 Then the area of the triangle is
10:05View SolutionThe line x + y = p, x and y axis meet at A and B respectively. A triangle APQ that is right-angled at Q is under the triangle OAB, where 0 is the origin. P and Q are located at OB and AB respectively. If the area of triangle APQ is 3/8 of the area of triangle OAB, then (AQ)/(BQ) Is equal -
02:05View SolutionIn the isosceles triangle OAB, O is the origin, OA=OB=6. If the equation of side AB is x−y+1=0, then the area of the triangle OAB is (in square units)
04:14View Solution