Question

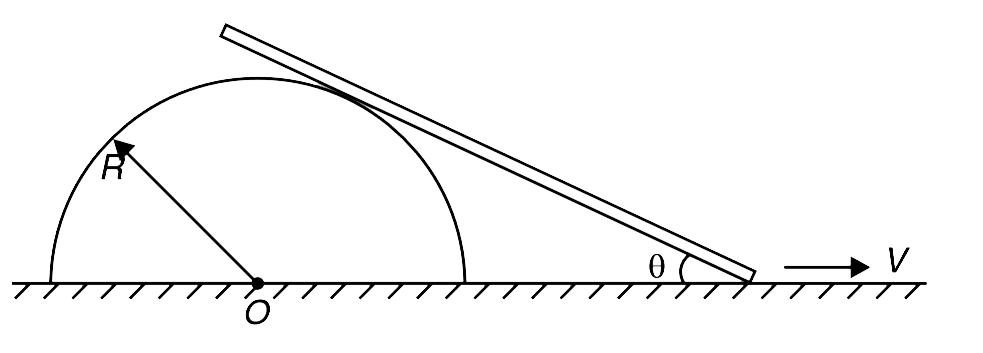
A rod AB is moving on a fixed circle of radius R with constant velocity ${\displaystyle v}$ as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance${\displaystyle x=\frac{3R}{5}}$ from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
(i) Find the speed of point of intersection P.
(b) Find the angular speed of point of intersection P with respect to centre of the circle.

Answer

14x+23y-40=0

Explanation

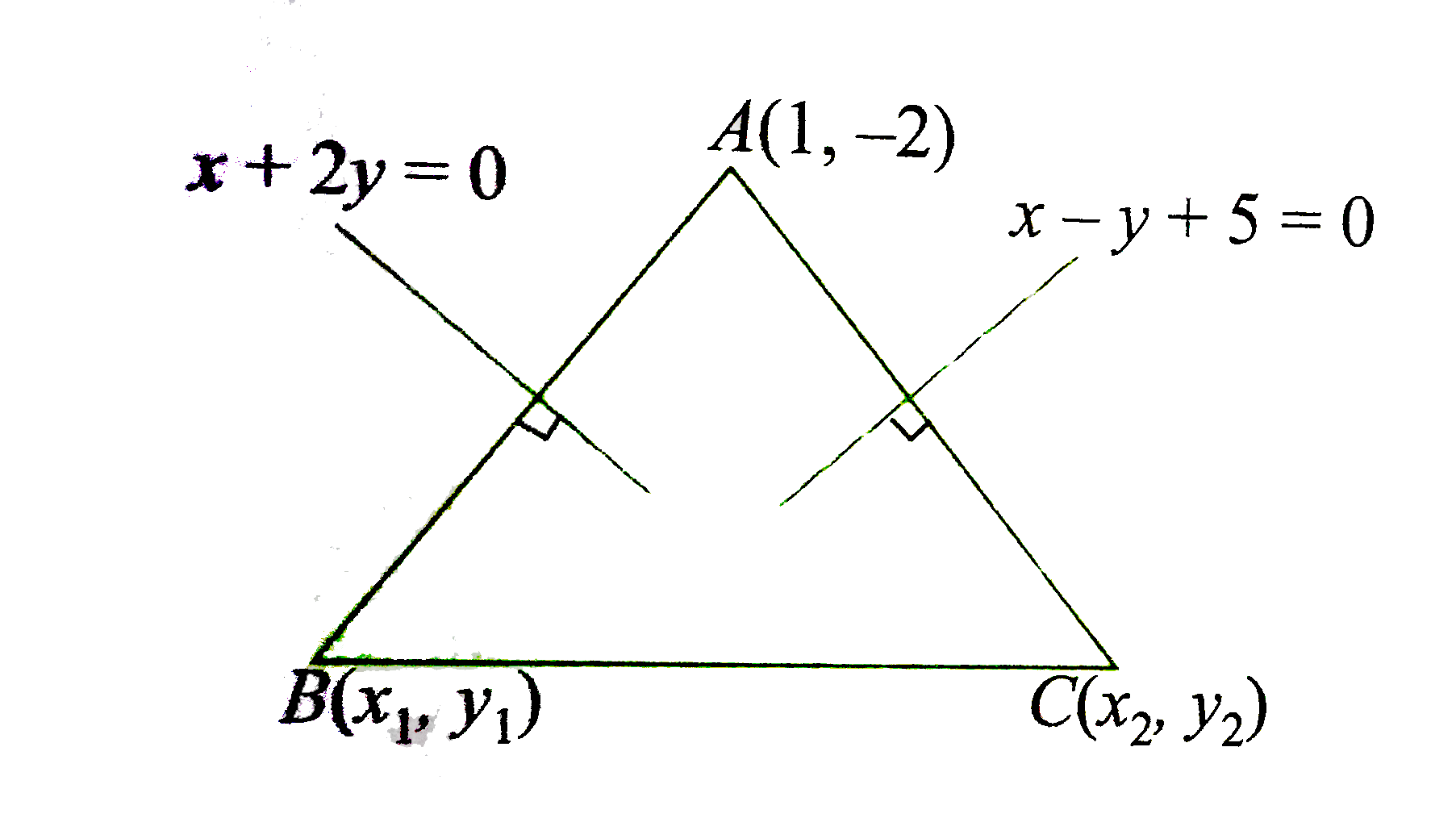
Since the given lines are perpendicular bisectors of the sides as shown in the figure, point B and C are the images of the point A in these lines. Therefore,
`(x_(1)-1)/(1) = (y_(1)-2)/(2) = -(2(1-4))/(1+4)`
`"and " (x_(2)-1)/(1) = (y_(2)+2)/(-1) = -(2(1+2+5))/(1+1)`
`therefore B(x_(1), y_(1))-= (11//5, 2//5) " and " C(x_(2), y_(2))-= (-7,6)`
Hence, the line passing through the points B and C is 14x+23y-40=0.