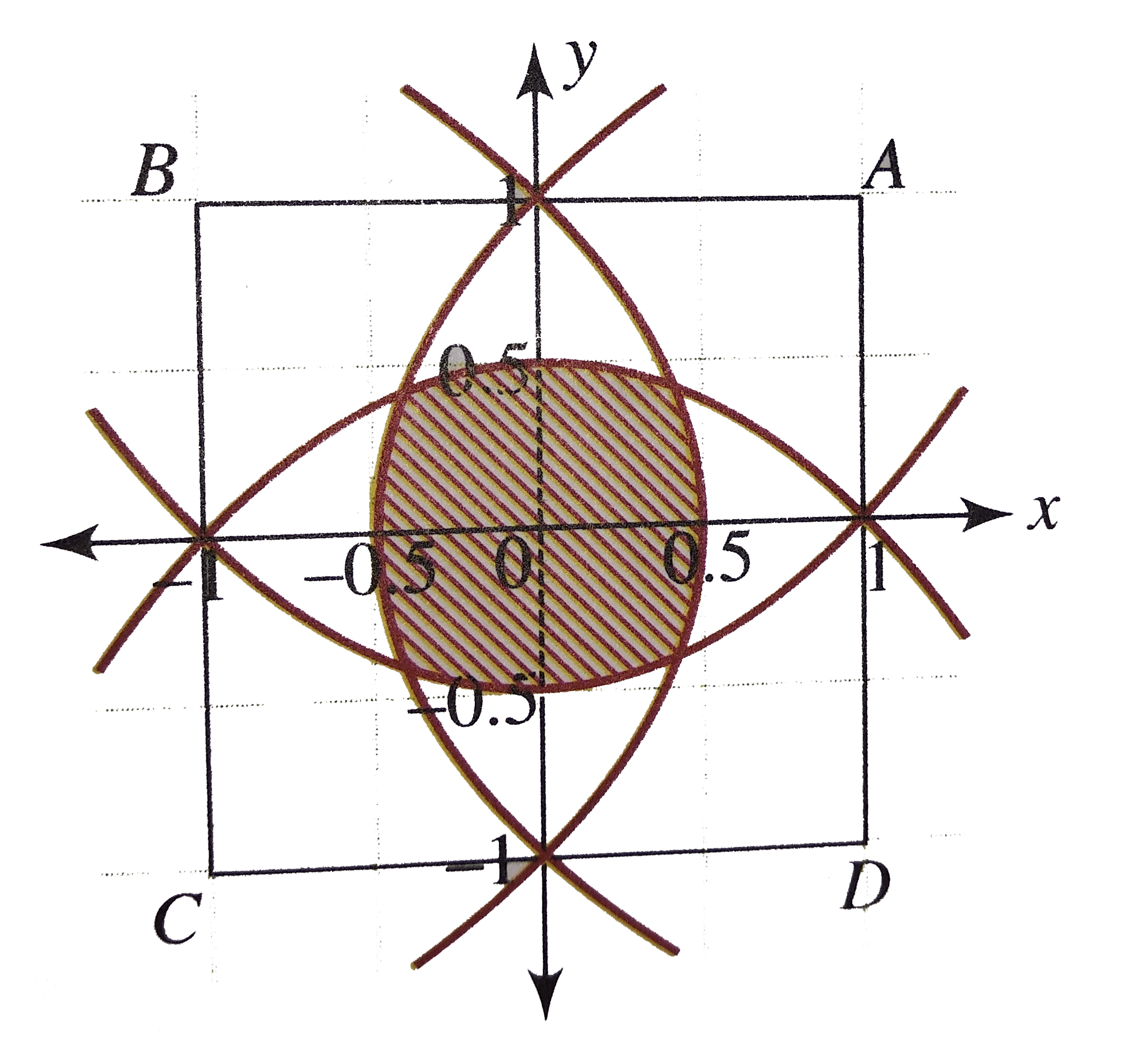
Consider a square with vertices at (1,1),(−1,1),(−1,−1),and(1,−1). Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.Solution in Bengali
Let us consider any point (x,y) inside the square such that its distance from the origin ≤ its distace from any of the edges, say AD.
∴ OP<PM
⇒ √(x2+y2)<1−x
⇒ y2≤−2(x−12) (i)
Above represents all points within and on the parabola P1.
If we consider the edges BC, then OP<PN will imply
y2≤2(x+12) (ii)
Similarly, if we consider the edges AB and CD, we will have
x2≤−2(y−12) (iii)
x2≤2(y+12) (iv)
Hence S consists of the region bounded by the four parabolas meeting the axes at (±12,0)and(0,±12).

Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionFind the equation of the ellipse that passes through the origin and has the foci at the points (−1,1)andS'(1,1).
View SolutionThe points A(5,−1,1),B(7,−4,7),C(1,−6,10)andD(−1,−3,4) are the vertices of a (A) rhombus (B) square (C) rectangle (D) none of these
View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.
View Solutionबिन्दुओ(1,1),(1,−1),(−1,1) और से बने त्रिभुज के क्षेत्रफल……….. वर्ग इकाई है ।
View SolutionConsider a square with vertices at (1,1)(−1,1)(−1,−1)and(1,−1). Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionFind the product [−1−1−11][1111]
View Solutionमाना वर्ग के शीर्ष (1,1),(−1,1),(−1,−1) तथा (1,−1) है | माना वर्ग के अन्दर के सभी बिन्दुओ मूल बिन्दु से किसी भी भुजा कि अपेक्षा पास हो, का क्षेत्र S है | S को क्षेत्र बनाइए तथा इसका क्षेत्रफल ज्ञात कीजिए |
View SolutionConsider a square with vertices at (1,1)(−1,1)(−1,−1)and(1,−1). Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionConsider a square with vertices at (1,1),(−1,1),(−1,−1),and(1,−1). Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionConsider a square with vertices at (1,1),(−1,1),(−1,−1),and(1,−1). Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.
View SolutionFind the distance between the following pairs of point:Q(3,2,−1)and B(−1,1,−1).
View SolutionSketch the region bounded by the curves y=x2+2, y=x, x=0 and x=1. also, find the area of this region.
View Solution
