Consider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.
The correct Answer is:643 sq. units
To find the area of the region common to R1 and R2, we will follow these steps:
Step 1: Define the regions mathematically.
Region R1: Points P are nearer to (1,0) than to the line x=−1.
The distance from a point P(x,y) to (1,0) is given by:
d1=√(x−1)2+y2
The distance from P(x,y) to the line x=−1 is:
d2=|x+1|
Since we want points nearer to (1,0) than to x=−1, we have:
d1<d2
Squaring both sides (since both distances are non-negative):
(x−1)2+y2<(x+1)2
Expanding both sides:
x2−2x+1+y2<x2+2x+1
Simplifying:
y2<4x
This represents the area inside the parabola y2=4x.
Region R2: Points P are nearer to (0,0) than to (8,0).
The distance from P(x,y) to (0,0) is:
d1=√x2+y2
The distance from P(x,y) to (8,0) is:
d2=√(x−8)2+y2
We want:
d1<d2
Squaring both sides:
x2+y2<(x−8)2+y2
Simplifying:
x2+y2<x2−16x+64+y2
Cancelling y2 and x2:
0<−16x+64
Rearranging gives:
16x<64⇒x<4
This represents the area to the left of the vertical line x=4.
Step 2: Find the area of the common region.
The common region is bounded by the parabola y2=4x and the line x=4.
To find the area, we will integrate from x=0 to x=4.
The upper half of the parabola is given by:
y=√4x
The area A can be calculated as:
A=2∫40√4xdx
Calculating the integral:
A=2∫402√xdx=4∫40x1/2dx
Using the power rule for integration:
=4(x3/23/2)40=4(23x3/2)40=83(43/2−0)
Calculating 43/2=8:
=83⋅8=643
Thus, the area of the common region is:
Area=643 square units
d1=√(x−1)2+y2
The distance from P(x,y) to the line x=−1 is:
d2=|x+1|
Since we want points nearer to (1,0) than to x=−1, we have:
d1<d2
Squaring both sides (since both distances are non-negative):
(x−1)2+y2<(x+1)2
Expanding both sides:
x2−2x+1+y2<x2+2x+1
Simplifying:
y2<4x
This represents the area inside the parabola y2=4x.
d1=√x2+y2
The distance from P(x,y) to (8,0) is:
d2=√(x−8)2+y2
We want:
d1<d2
Squaring both sides:
x2+y2<(x−8)2+y2
Simplifying:
x2+y2<x2−16x+64+y2
Cancelling y2 and x2:
0<−16x+64
Rearranging gives:
16x<64⇒x<4
This represents the area to the left of the vertical line x=4.
y=√4x
The area A can be calculated as:
A=2∫40√4xdx
Calculating the integral:
A=2∫402√xdx=4∫40x1/2dx
Using the power rule for integration:
=4(x3/23/2)40=4(23x3/2)40=83(43/2−0)
Calculating 43/2=8:
=83⋅8=643
Area=643 square units
Topper's Solved these Questions
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Exercises - Single Correct Answer Type
Explore 40 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Multiple Correct Answers Type
Explore 13 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Concept Application Exercise 9.2
Explore 14 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGE ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Comprehension Type
Explore 5 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
Similar Questions
Consider two regions: R1: Point P is nearer to (1,0) then to x=−1. R2: Point P is nearer to (0,0) then to (8,0). Then which of the following statements are true: Statement1: The area of the region common to R1andR2 is 1283sq.units. Statement2 : The area bounded by x=4√yandy=4 is 323sq.units.
View SolutionConsider the points P(2,−4);Q(4,−2)andR(7,1). The points P,Q,R
View Solution
Knowledge Check
Consider two conductinbg spheres of radill R1andR2 with R1>R2. If the two are at the same potential, and the larger sphere has more charge than the smaller sphere, then
Athe charge density of smaller sphere is less then that of larger sphere,Bthe charge density of smaller sphere is more than that of larger sphere.Cboth spheres may have same charge density.Dnone of these
Plot point P(1,0),Q(4,0)andS(1,3). Find the coordinates of R so that PQRS is a square.
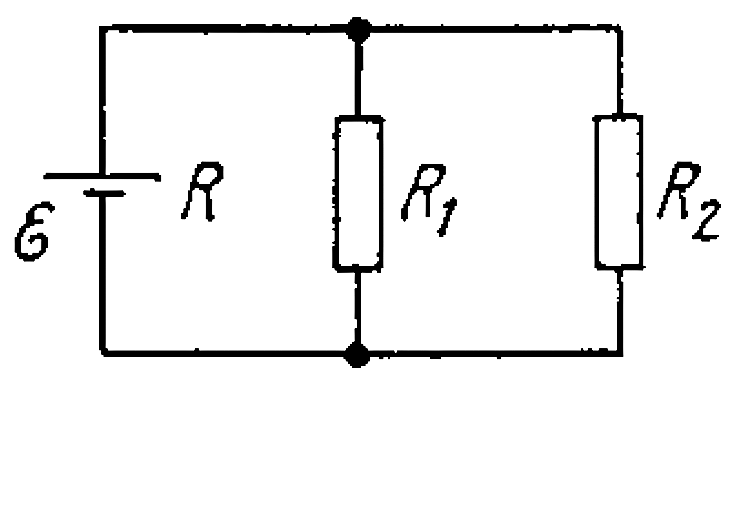
View SolutionIn the circuit shown in Fig. the emf of the sources is equal to ξ=5.0V and the resistances are equal to R1=4.0Ω and R2=6.0Ω. The internal resistance of the source equals R=1.10Ω. Find the currents flowing through the resistances R1 and R2.
View SolutionNormals of parabola y2=4x at P and Q meets at R(x2,0) and tangents at P and Q meets at T(x1,0). If x2=3, then find the area of quadrilateral PTQR.
View SolutionFind the value of ∞∑r=0tan−1(11+r+r2)
View SolutionLet P be a plane passing through the points (2,1,0) (4,1,1) and (5,0,1) and R be any point (2,1,6) . Then the image of R in the plane P is :
View SolutionIn a parallelogram PQRS (taken in order), P is the point (-1, -1), Q is (8, 0) and R is (7, 5). Then S is the point :
View SolutionLet f:[1,2]→[0,∞) be a continuous function such that f(x)=f(1−x) for all x∈[−1,2]. Let R1=∫2−1xf(x)dx, and R2 be the area of the region bounded by y=f(x),x=−1,x=2 and the x-axis . Then,
View Solution