For a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, isSolution in Bengali
For P(x,y), we have
2≤d1(P)+d2(P)≤4
⇒ 2≤|x−y|√2+|x+y|√2≤4 ltBrgt ⇒ 2√2≤|x−y|+|x+y|≤4√2
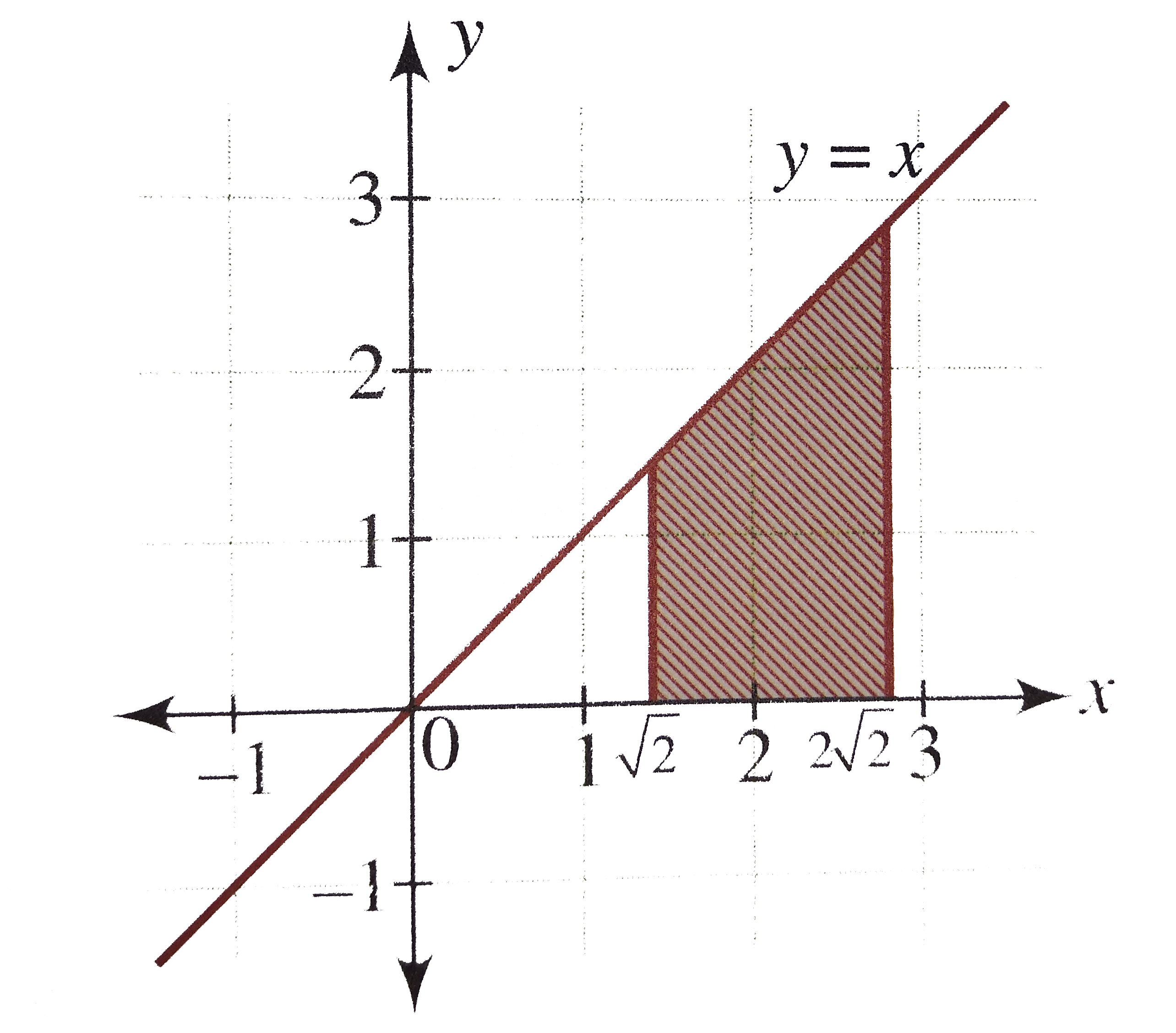
In the first quadrant if x>y, we have
2√2≤x−y+x+y≤4√2
or √2≤x≤2√2
The region of points satisfying these inequalities is as follows.
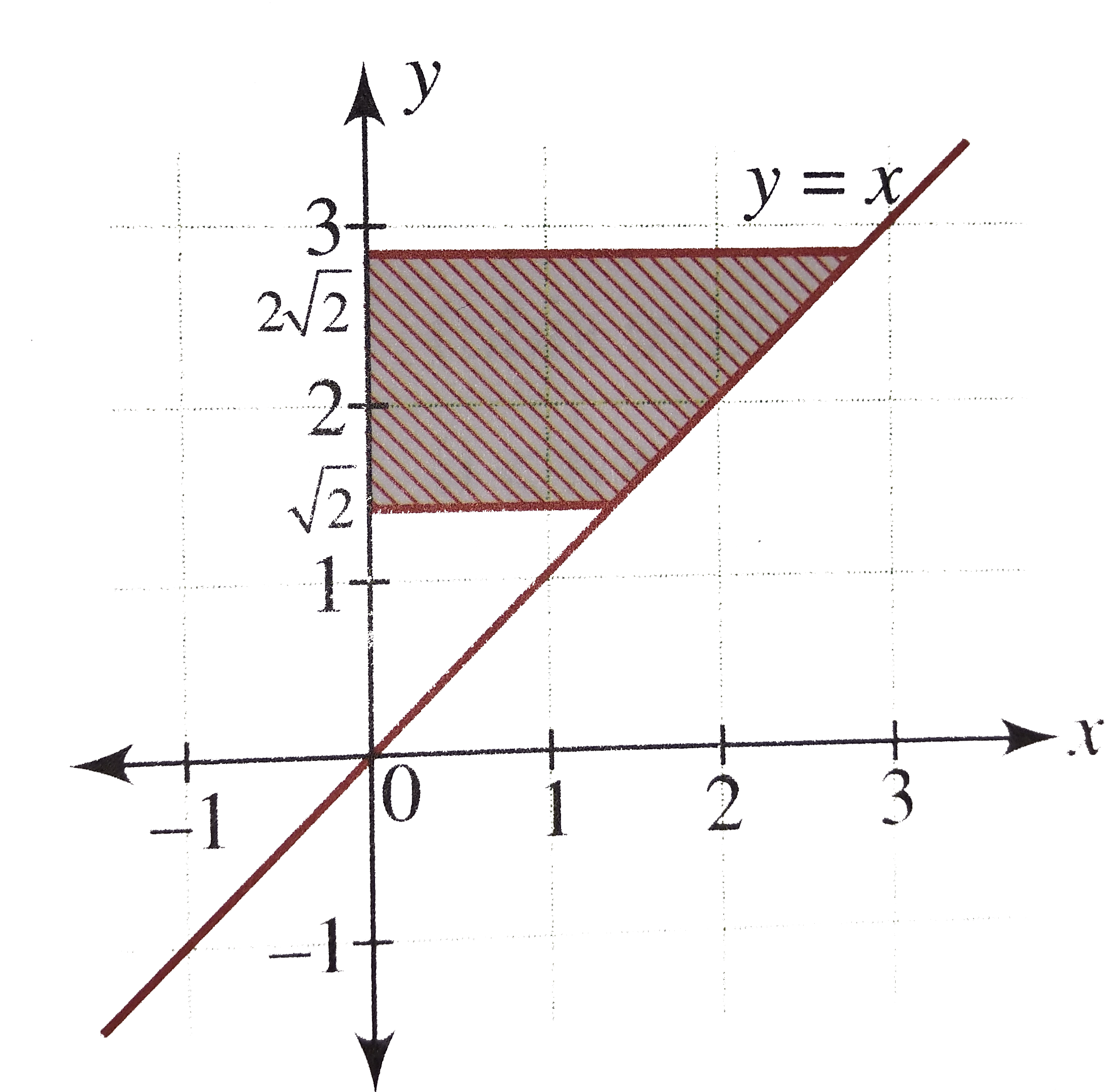
In the first quadrant if x<y, we have
2√2≤y−x+y≤4√2
or √2≤y≤2√2
The region of points satisfying these inequalities is as follows.
Combining the above two regions, we have the following.
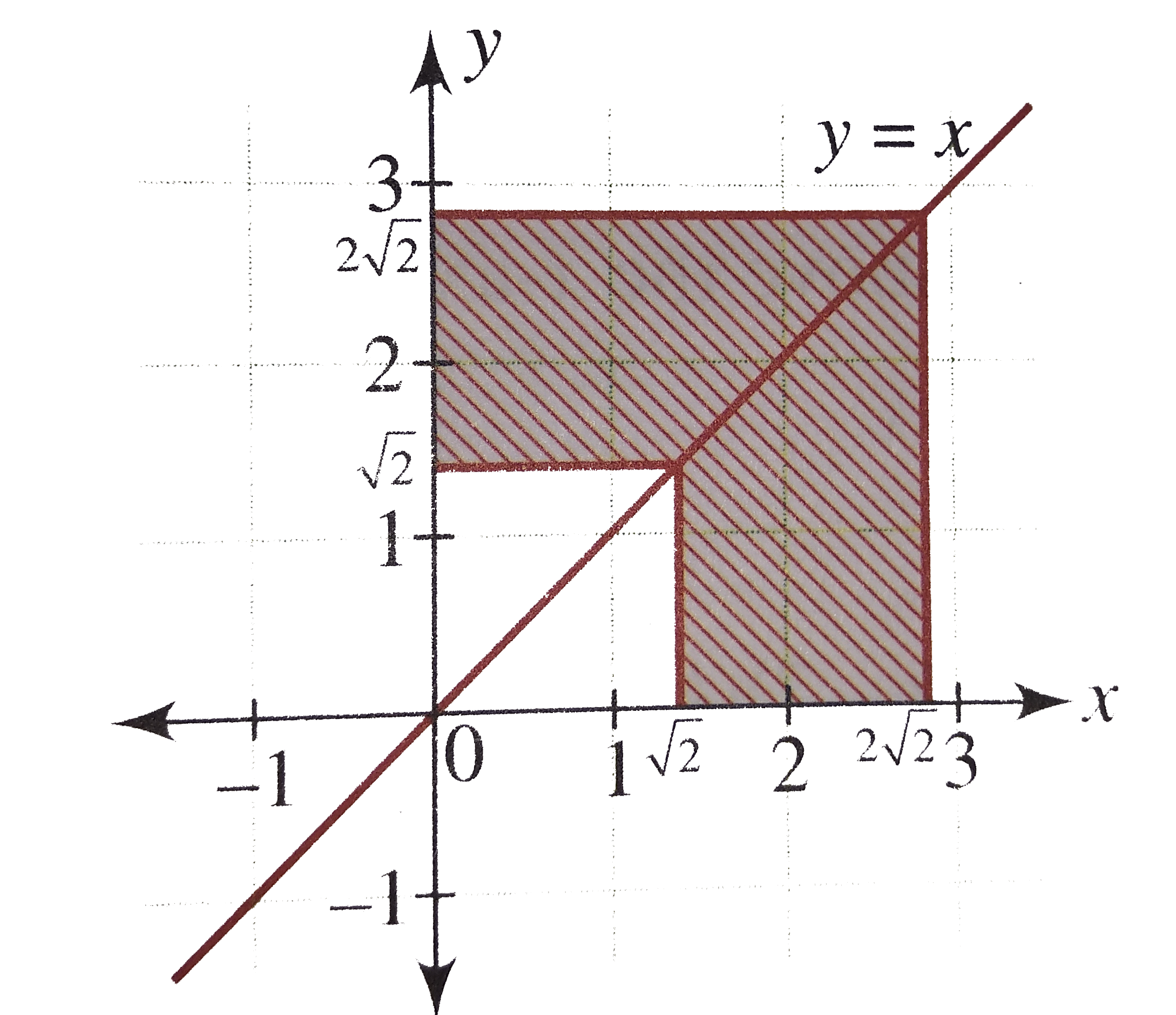
Area of the shaded region =((2√2)2−(√2)2)
=8−2=6 sq.units
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionFor a point P in the plane, let d1 (P) and d2 (P) be the distance of the point P from the lines x – y = 0 and x + y = 0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2 < d1(P) + d2 (P)< 4, is
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionConsider two lines L1andL2 given by x−y=0 and x+y=0 , respectively, and a moving point P(x,y). Let d(P,L1),i=1,2, represents the distance of point P from the line Lt If point P moves in a certain region R in such a way that 2≤d(P,P1)+d(P,L1)≤4 , find the area of region R.
View SolutionFor a point P(x,y),x<=2 in x-y plane moves on path y=|ax-1|+|ax-2|+ax AA alpha in[0,1] If area of region R consisting of all points P lying in the first quadrant of the plane is A when take it's all values alpha in[0,1], then value of (6)/(A) is
View SolutionFor a point P in the plane let d1(P)andd2 be the distance of the point P from the lines x−y=0 R consisting of all points P lying in the first quadrant of the plane and satisfying 2≥d1(P)+d2(P)≥4, is
View SolutionFor a point P in the plane, let d1(P) and d2(P) be the distances of the point P from the lines x−y=0 and x+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View Solutionसमतल में स्थित किसी बिन्दु P से रेखाओ x - y = 0 तथा x + y = 0 की दुरी क्रमशः d1(P) तथा d2(P) है। यदि क्षेत्र R उन सभी बिन्दुओ P से बना है जो प्रथम चतुर्थांश (quadrant) में स्थित है तथा 2≤d1(P)+d2(P)≤4 को संतुष्ट करते है, तब क्षेत्र R का क्षेत्रफल है
View SolutionFor a point P in the XY plane.Let d1(p),d2(p) and d3(p) be the distances of the point P from the x axis,y axis and x−y=0 respectively. If A is area of the region R consisting of all points P lying in the XY plane and satisfying d1(P)+d2(P)+√2d3(P)=5 then Which of the following is/are CORRECT
View Solutionসমতল p:x−y+z=5 এবং একটি বিন্দু P(1,−2,3)P বিন্দু থেকে সমতল p-এর দূরত্ব-
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionConsider two lines L1andL2 given by x−y=0 and x+y=0 , respectively, and a moving point P(x,y). Let d(P,L1),i=1,2, represents the distance of point P from the line Lt If point P moves in a certain region R in such a way that 2≤d(P,L1)+d(P,L2)≤4 , find the area of region R.
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionThe distance of the lines xy = 0 and x + y = 0 from a point P located in the plane respectively d_(P) And d_2(P) is. If area R is made up of all the points P which lie in the first quadrant and satisfy 25d (P) + d2 (P) 34, the area of fixed area R is
View Solution
