For a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, isSolution in Tamil
For P(x, y), we have
2≤d1(P)+d2(P)≤4
⇒2≤|x−y|√2+|x+y|√2≤4
2√2≤|x−y|+|x+y|≤4√2
In first quadrant, if x>y, we have
2√2≤x−y+x+y≤4√2
or √2≤x≤2√2
The region of points satisfying these inequalities is
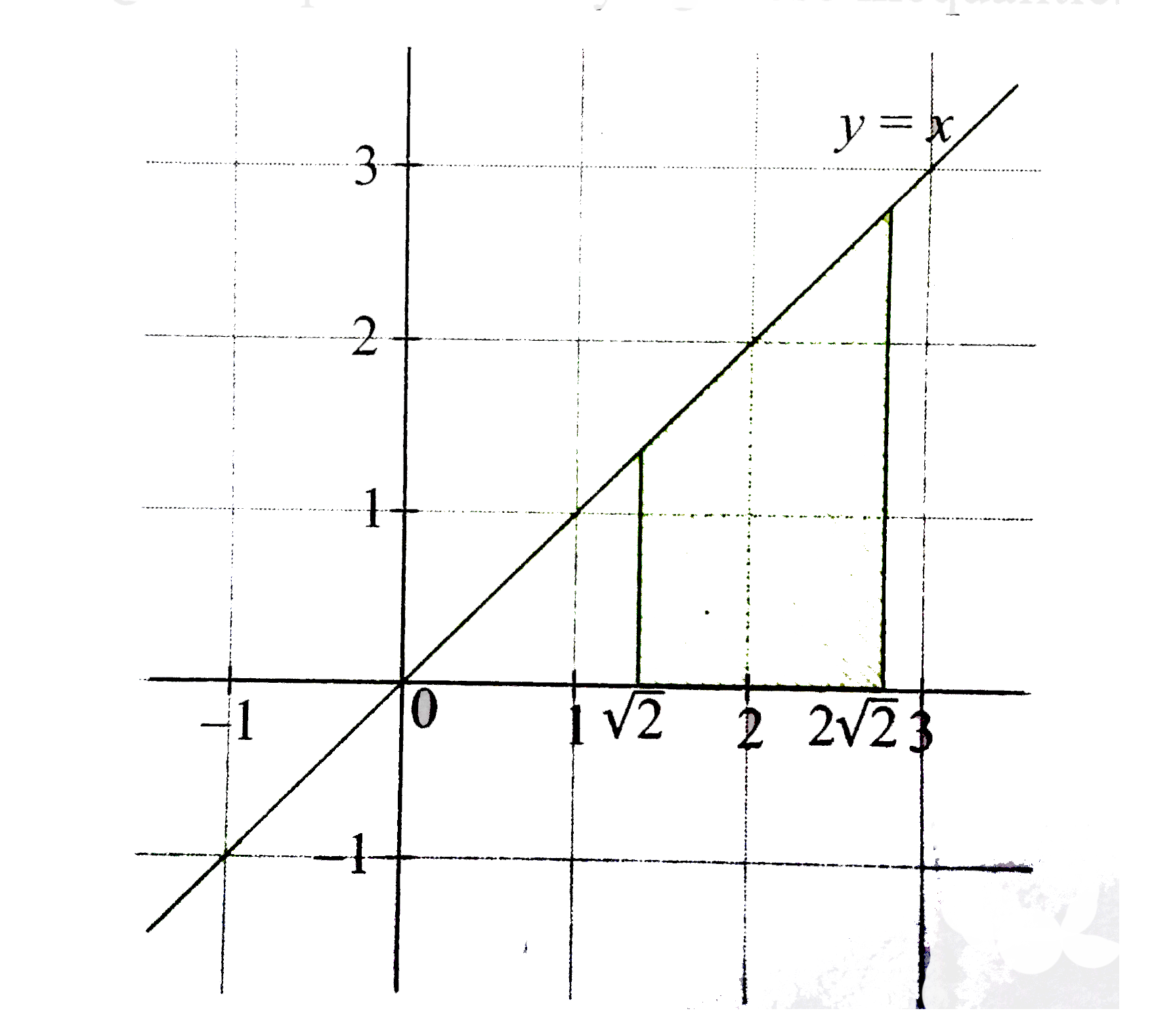
In first quadrant, if x<y, we have
or √2≤y≤2√2
The region of points satisfying these inequalities is
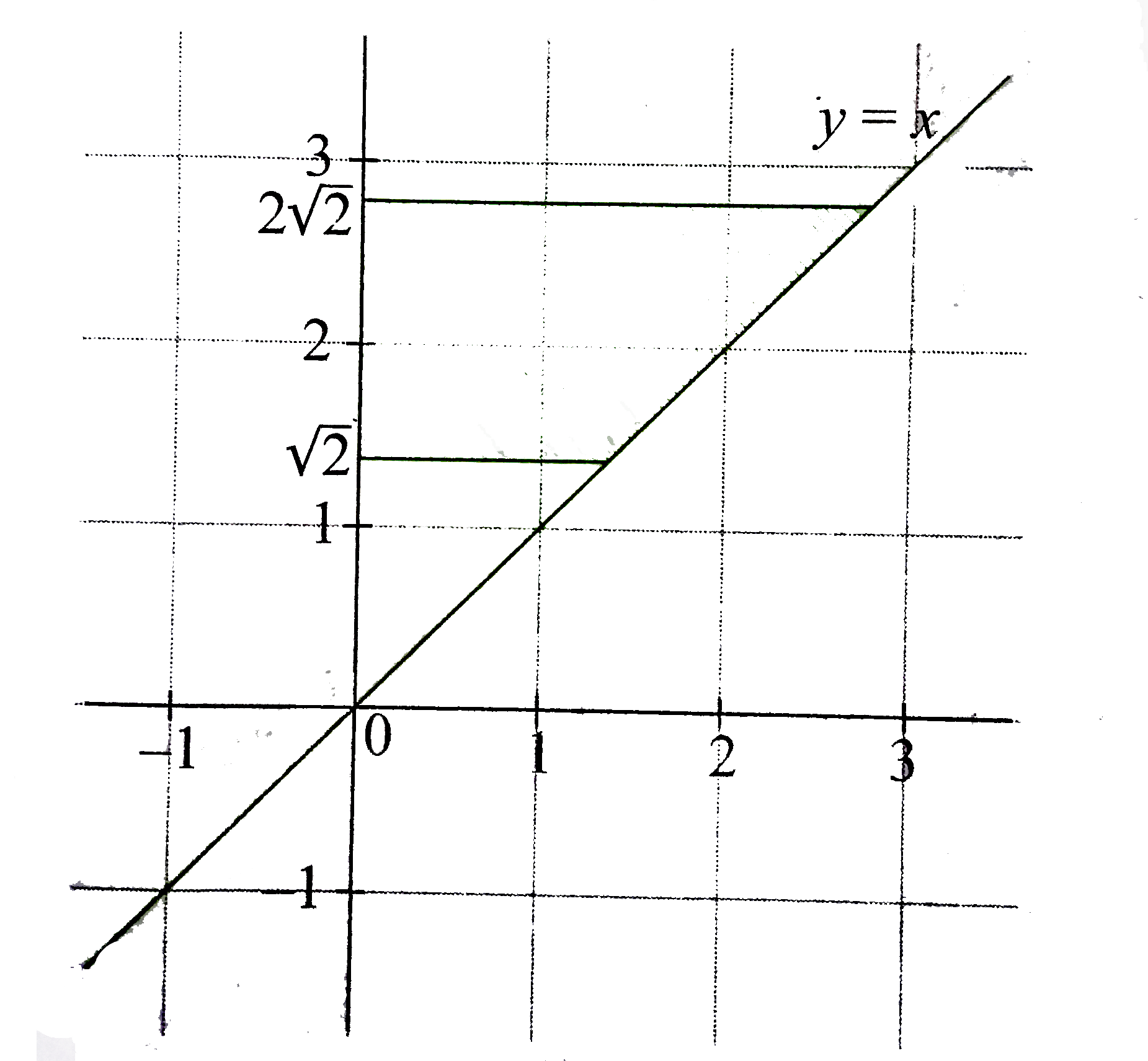
Combining above two regions, we have
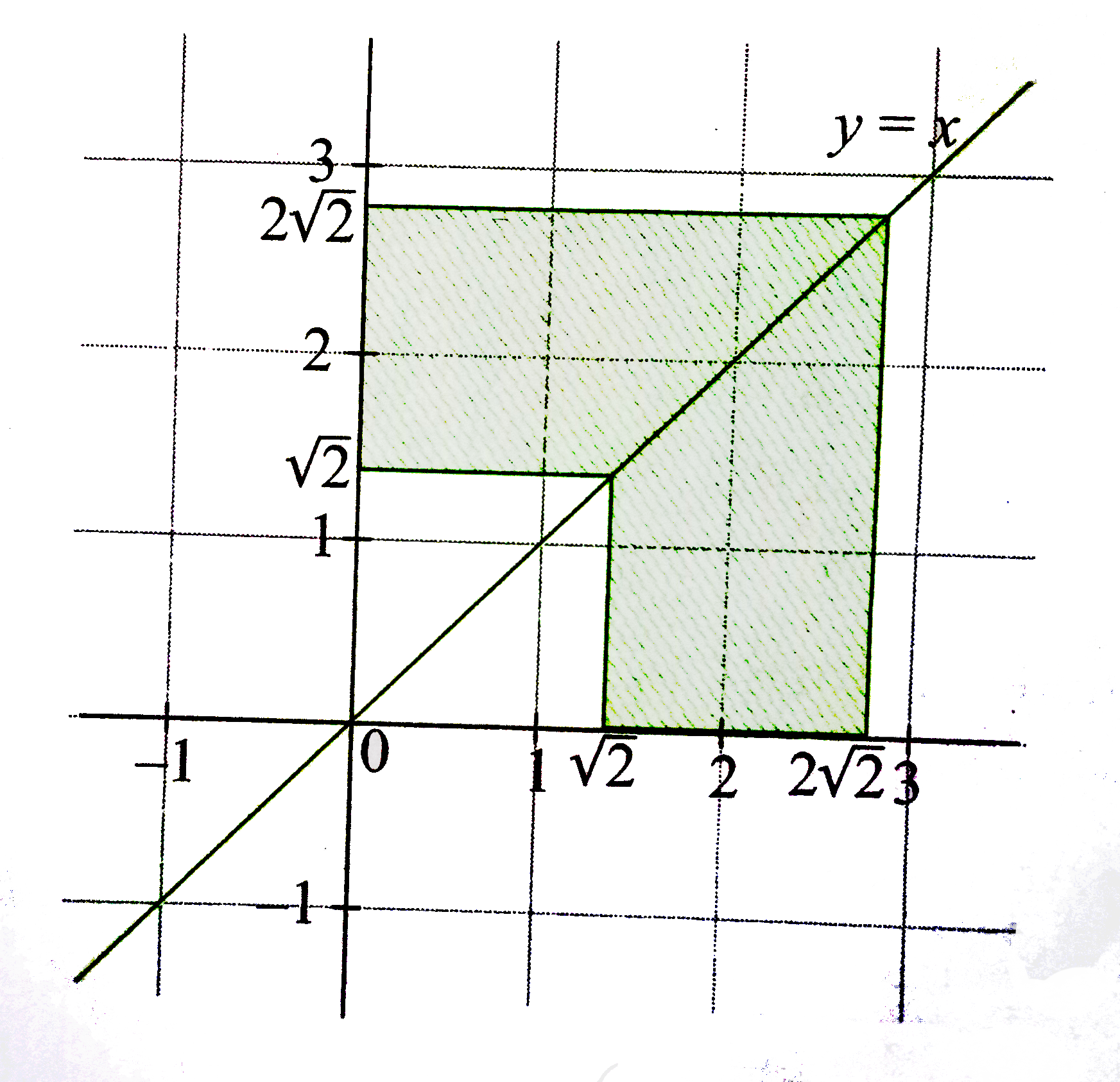
Area of shaded region =((2√2)2−(√2)2)
=8-2= 6 sq. units
Topper's Solved these Questions
Similar Questions
The line L given by x5+yb=1 passes through the point (13,32).the line K is parallel to L and has the equation xc+y3=1 then the distance between L and K is
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionFor a point P in the plane, let d1 (P) and d2 (P) be the distance of the point P from the lines x – y = 0 and x + y = 0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2 < d1(P) + d2 (P)< 4, is
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionConsider two lines L1andL2 given by x−y=0 and x+y=0 , respectively, and a moving point P(x,y). Let d(P,L1),i=1,2, represents the distance of point P from the line Lt If point P moves in a certain region R in such a way that 2≤d(P,P1)+d(P,L1)≤4 , find the area of region R.
View SolutionFor a point P(x,y),x<=2 in x-y plane moves on path y=|ax-1|+|ax-2|+ax AA alpha in[0,1] If area of region R consisting of all points P lying in the first quadrant of the plane is A when take it's all values alpha in[0,1], then value of (6)/(A) is
View SolutionFor a point P in the plane let d1(P)andd2 be the distance of the point P from the lines x−y=0 R consisting of all points P lying in the first quadrant of the plane and satisfying 2≥d1(P)+d2(P)≥4, is
View SolutionFor a point P in the plane, let d1(P) and d2(P) be the distances of the point P from the lines x−y=0 and x+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View Solutionसमतल में स्थित किसी बिन्दु P से रेखाओ x - y = 0 तथा x + y = 0 की दुरी क्रमशः d1(P) तथा d2(P) है। यदि क्षेत्र R उन सभी बिन्दुओ P से बना है जो प्रथम चतुर्थांश (quadrant) में स्थित है तथा 2≤d1(P)+d2(P)≤4 को संतुष्ट करते है, तब क्षेत्र R का क्षेत्रफल है
View SolutionFor a point P in the XY plane.Let d1(p),d2(p) and d3(p) be the distances of the point P from the x axis,y axis and x−y=0 respectively. If A is area of the region R consisting of all points P lying in the XY plane and satisfying d1(P)+d2(P)+√2d3(P)=5 then Which of the following is/are CORRECT
View Solutionসমতল p:x−y+z=5 এবং একটি বিন্দু P(1,−2,3)P বিন্দু থেকে সমতল p-এর দূরত্ব-
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionConsider two lines L1andL2 given by x−y=0 and x+y=0 , respectively, and a moving point P(x,y). Let d(P,L1),i=1,2, represents the distance of point P from the line Lt If point P moves in a certain region R in such a way that 2≤d(P,L1)+d(P,L2)≤4 , find the area of region R.
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View Solution
