Consider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.Solution in Tamil
The correct Answer is:643 sq. units
R1: points P(x,y) are nearer to (1,0) than to x=-1
∴ √(x−1)2+y2<|x+1|
⇒ y2<4x
⇒ point P lie inside parabola y2=4x
R2: Points P(x,y) are nearer to (0,0) than to (8,0)
∴ |x|<|x−8|
⇒ x2<x2−16x+64
⇒ x<4
⇒ point P lie to the left side of line x=4
The area of common region of R1andR2 is area bounded by x=4 and y2=4x.
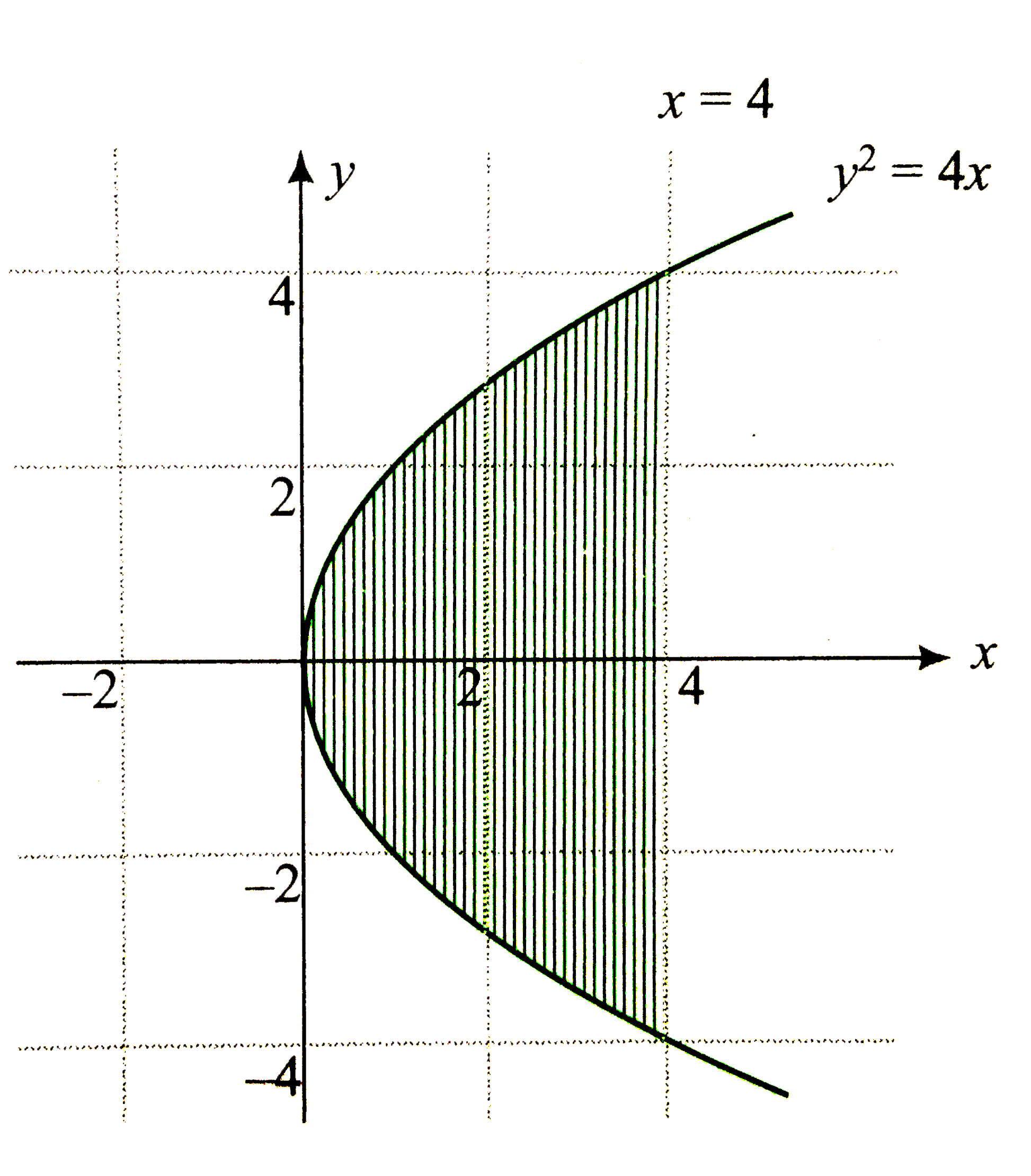
∴ Required area =24∫0(4−y24)dy (Integrating along x-axis)
=2[4y−y312]40
=2[16−6412]
643 sq. units
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)40videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)10videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Area enclosed by the curve y=f(x) defined parametrically as x=1−t21+t2,y=2t1+t2isequa<o πsq.units (b) π2sq.units 3π4sq.units (d) 3π2sq.units
01:00View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
06:07View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
06:14View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
03:01View SolutionA=[[1,0-1,3]],R_(1)harr R_(2)
10:10View SolutionThree circles with radius r1,r2,r3 touch one another externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 2. The value of (r1r2r3r1+r2+r3) is equal to
01:44View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.03:39View SolutionConsider two conductinbg spheres of radill R1andR2 with R1>R2. If the two are at the same potential, and the larger sphere has more charge than the smaller sphere, then
03:29View Solutionयदि समीकरण x2−px+(p−1)=0 के मूल r1 तथा r2 है, तब p के कौन - से मान के लिए (r21+r22) का मान अल्पतम होगा ?
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
03:28View Solutionयदि दो बहुभुज प्रदेश R1 और R2 इस प्रकार संबद्ध हो कि R1,R2 का एक खंड हो, तो निम्नलिखित में कौन सत्य है?
03:22View SolutionThe formula –G Mm (1//r_(2) – 1//r_(1)) is more/less accurate than the formula mg (r_(2) – r_(1)) for the difference of potential energy between two points r_(2) and r_(1) distance away from the centre of the earth.
01:59View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.05:42View SolutionTake two fields R_(1): x=-1 P is closer to point (1,0) than R: P is closer to point (8,0) than (0,0). Statement - 1 R_(1) " तथा " R_2 Area of common area of (128)/3 Unit. Statement - 2: x = 4sqrty And area enclosed by y = 4 (32)/3 Unit.
04:53View Solution
