Question

Let ${\displaystyle f\left(x\right)=\{\begin{array}{ll}{x}^2+3x\text{,}& -1\le x<0\\ -\sin x\text{,}& 0\le x<\pi /2\\ -1-\cos x\text{,}& \frac{\pi }{2}\le x\le \pi \end{array}}$ . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minima

Explanation

We have `f(x) = {{:(x^(2) + 3x",", -1 le x lt 0),(-sin x",", 0 le x lt pi//2),(-1 - cos x",", (pi)/(2) le x le pi):}`
`y = x^(2) + 3x`
`therefore` `y = (x + 3//2)^(2) - 9//4`
`therefore` `(y + 9//4) = (x + 3//2)^(2)` which is a parabola having vertex at `(-3//2, - 9//4)`.
For `y = - sin x, y = 0` when x = 0 and y = -1 when `x = pi//2`.
For y = -1 - cos x, y = -1 when `x = pi//2` and y = 0 when `x = pi`.
Hence the graph of the function y = f(x) is as shown in the following figure.

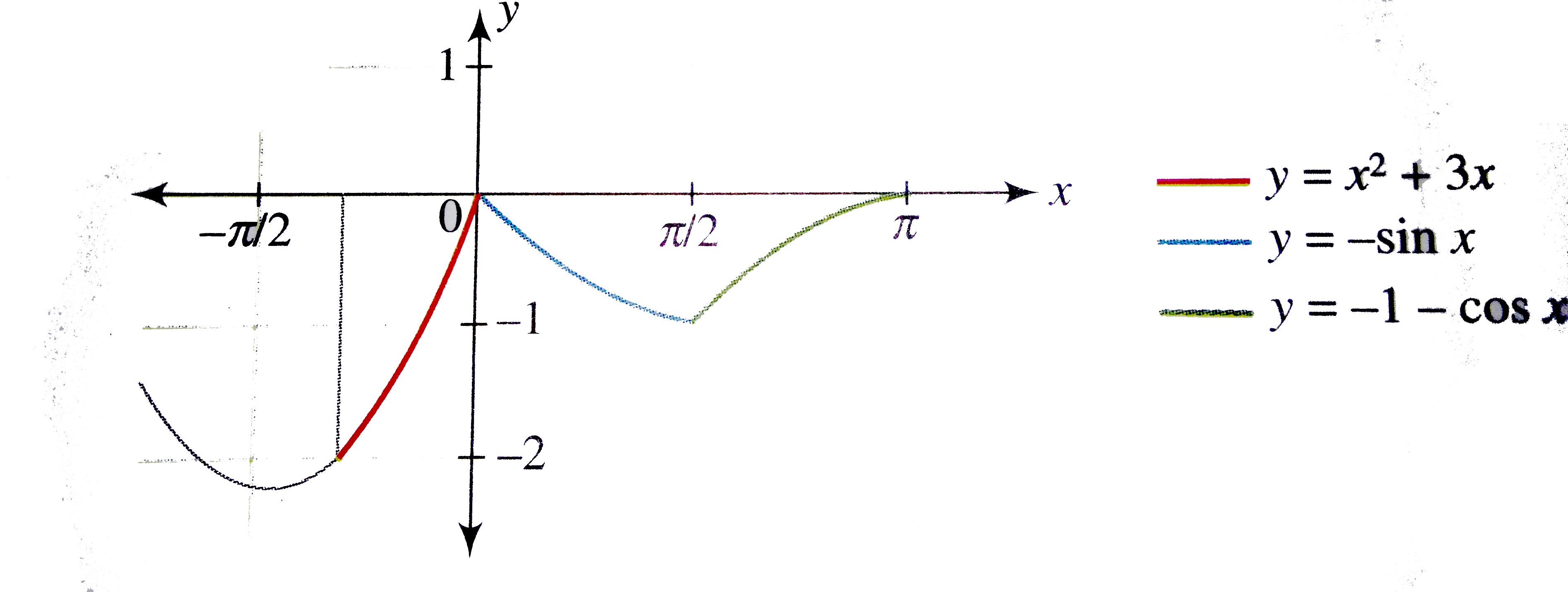
From the graph, `x = pi//2` is the point of local minima.
for `y = -sin x, y'' = sin x gt 0` for `x in (0, pi//2)`. SO the curve is concave upwards.
For `y = -1 - cos x, y'' = cos x lt 0` for `x in (pi//2, pi)`. So the curve is concave downwards.
Hence `x = pi//2` is the point of inflection.
The least value of `y = f(x)` occurs for `y = x^(2) + 3x`, when x = -1.
Hence the least value is -2. Therefore, the range is [-2, 0].