The number of roots of the equation is (a) 2 (b) 3 (c) 4 (d) 0Solution in Bengali
We have x sin x = 1
Number of roots of the above equation = number of points (s) of the intersection of the graphs of and for
The graphs of both functions are as shown in the following figure.
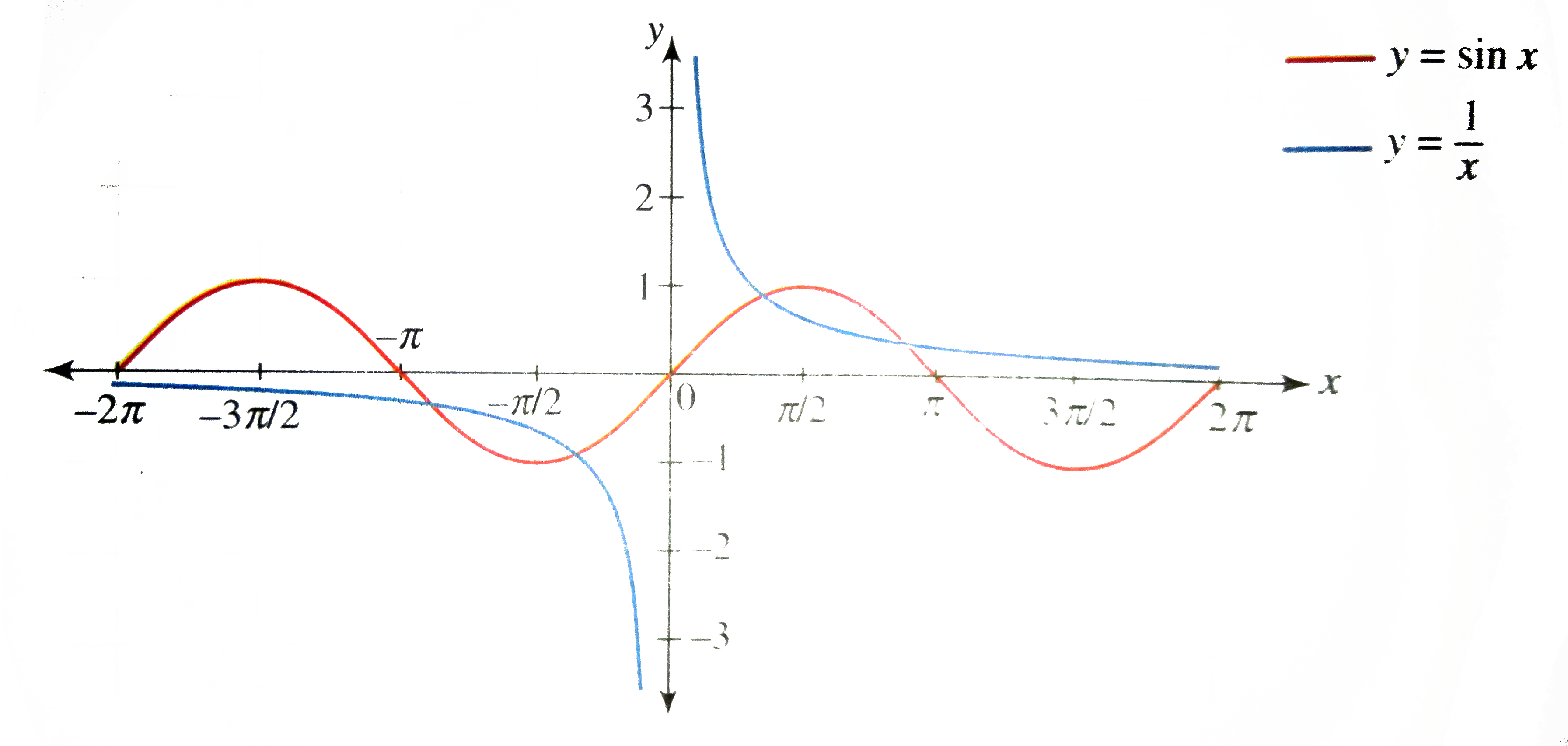
Graphs intersect at four points, hence four roots.
Related Playlists
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
03:52View SolutionDraw the graph of y=1(1/x).
01:52View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
01:16View SolutionThe number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is 2 (b) 3 (c) 4 (d) 0
03:12View SolutionThe number of real roots (s) of the equation x2tanx=1 lying between 0 and 2π is /are (A) 1 (B) 2 (C) 3 (D) 4
05:10View SolutionFind the number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π].
02:21View SolutionThe number of roots of the equation xsinx=1,,x∈[−2π,0]∪(0,2π) is
05:32View SolutionThe number of solutions of the equation tanx+secx=2cosx lying in the interval [0,2π] is 0 (b) 1 (c) 2 (d) 3
02:07View SolutionThe number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is (a) 2 (b) 3 (c) 4 (d) 0
02:52View SolutionIf the roots of the equation x2+ax+b=0arecandd, then roots of the equation x2+(2c+a)x+c2+ac+b=0 are a c b. d−c c. 2c d. 0
05:46View SolutionFind the number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π].
04:43View SolutionIf |cotx+cosecx|=|cotx|+|cosecx|,x∈[0,2π], then complete set of values of x is : (a).[0,π] (b).(0,π2] (c).(0,π2]∪[3π2,2π) (d).(π,3π2]∪[7π4,2π]
04:02View SolutionNumber of roots of equation 3|x|−|2−|x∣∣=1 is a. 0 b. 2 c. 4 d. 7
02:58View SolutionThe number of solution of equation 2cos−1x=a+a2(cos−1x)−1 are at least (a) 1 if a∈[−2π,π]−{0} (b) 1 if a ∈(0,π] (c) 1 if a∈[−2π,0) (d) 2 if a>0
03:25View SolutionNumber of roots of equation 3|x|−|2−|x∣∣=1 is a. 0 b. 2 c. 4 d. 7
04:23View SolutionThe number of real roots of the equation x2tanx=1 lies between 0and2π is/are
(A) 1 (B) 2 (C) 3 (D) 404:45View Solution


