Evaluate : [limx→0tanxx], where [⋅] represents the greatest integer function.Solution in Bengali
Let us first draw the graph of y = x and y = tan x.
For y=x,y'=1, i.e. the slope of the line is 1 for all real x.
For y=tanx,y'=sec2x
Thus, both y = x and y = tan x have slope '1' at x = 0, hence the graphs touch each other.
Moving from '0' to 'π/2' the values of sec2x increase from '1' to ∞.
Thus, the graph pf y = tan x lies below the graph of y = x.
The graphs of y = x and y = tan x are plotted as follows.
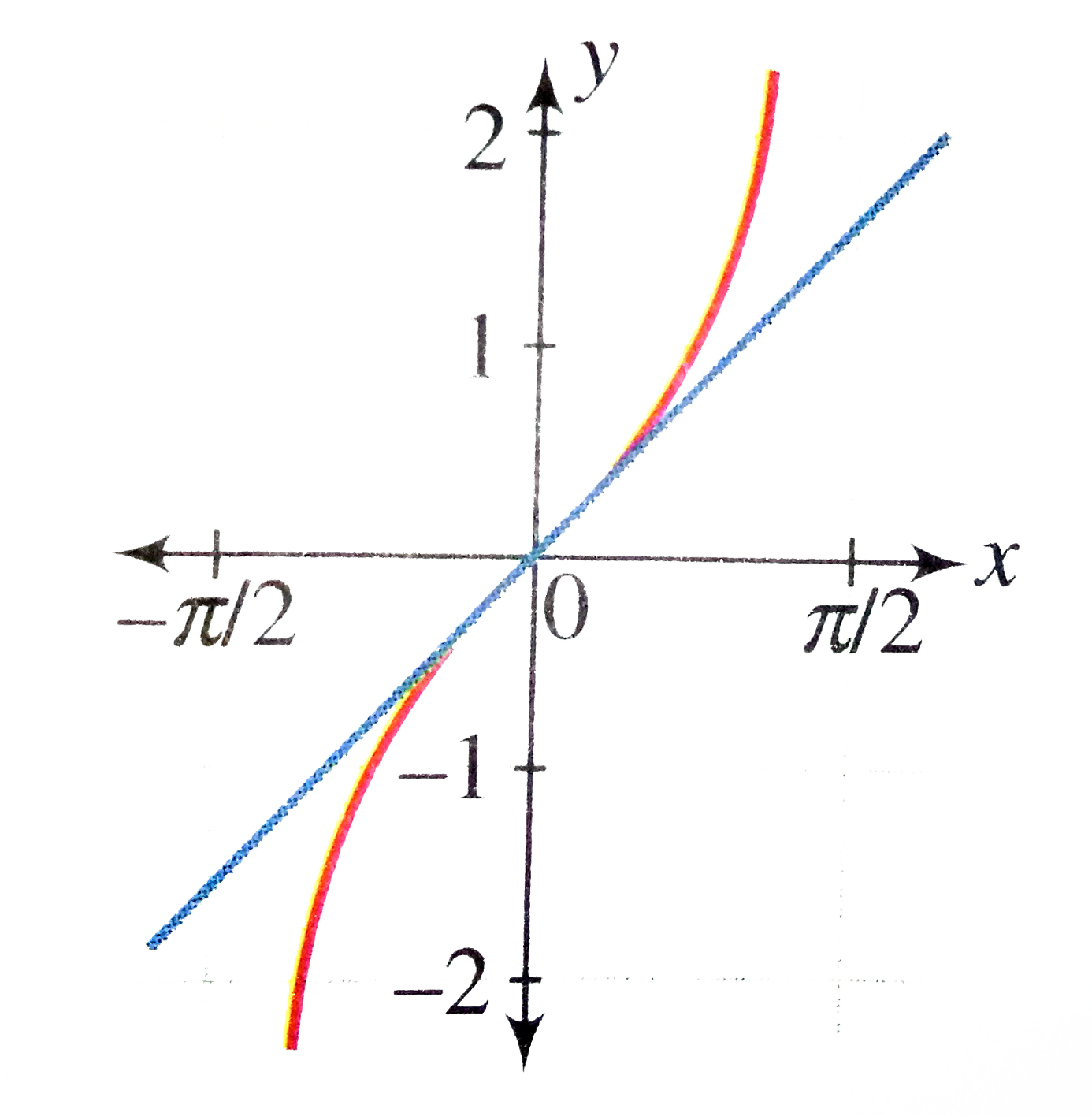
From the graph, when x→0+, the graph of y = tan x is above the graph of y = x
or tanx>x⇒tanxx>1⇒[limx→0+tanxx]=1
When x→0−, the graph of y = x is above the graph of y = tan x
or tanx<x⇒tanxx>1 (as x is negative) ⇒[limx→0+tanxx]=1
Thus, [limx→0tanxx]=1
Related Playlists
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
06:15View SolutionDraw the graph of y=1(1/x).
05:14View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
02:50View SolutionEvaluate: (lim)x→0sinxx,where[.] represents the greatest integer function.
02:15View SolutionEvaluate: (lim)x→0tanxx where [.] represents the greatest integer function
03:28View SolutionEvaluate: ∫10π0[tan−1x]dx,where[x] represents greatest integer function.
01:49View Solutionlim_(x rarr0)|x(x-1)|^([cos2x]), where [^(*)] represents the greatest integer function,is equal to
03:16View Solutionlim_(x rarr0)(tan^(2)[x])/([x]^(2)), where [] represents greatest integer function,is
01:33View SolutionThe value of lim_(x rarr pi)sgn[tan x], where [.] represents greatest integer function,
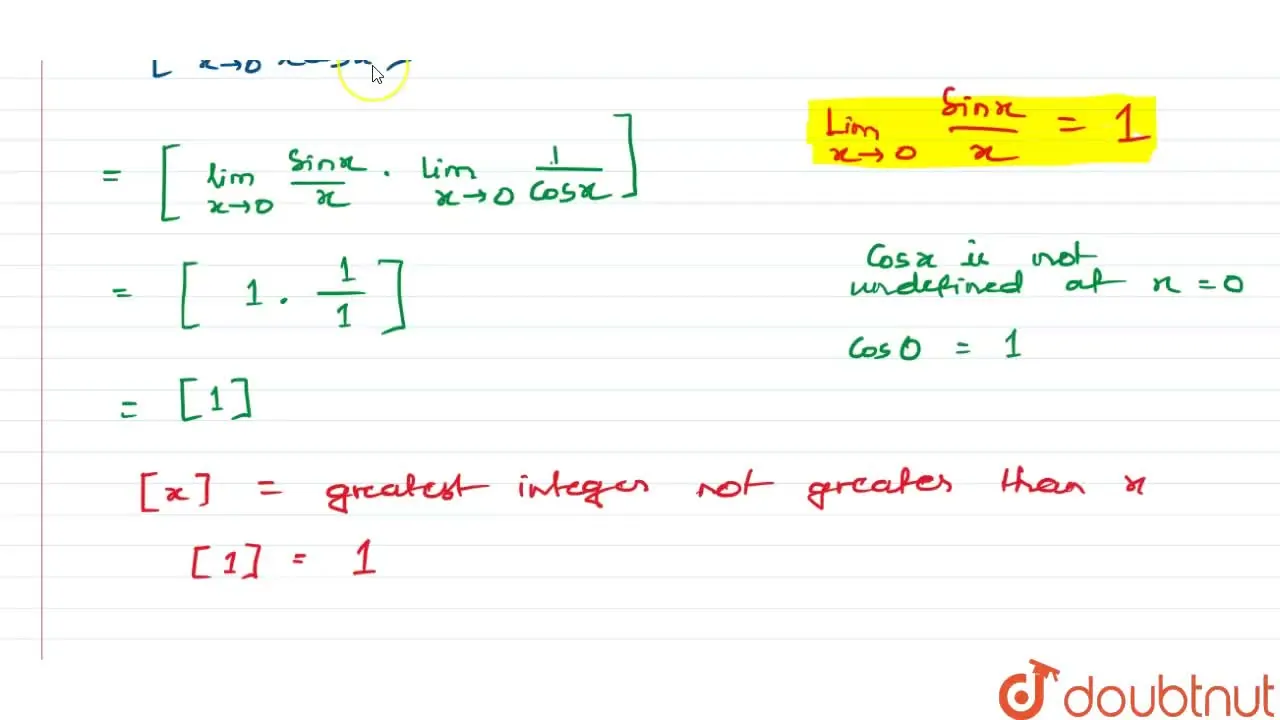
01:13View SolutionEvaluate : [limx→0sinxx], where [⋅] represents the greatest integer function.
03:38View SolutionThe value of limx→0[xsinx] , where [.] represents the greatest integer function,is
02:03View Solutionlimx→0[100tanxsinxx2] is (where [.] represents greatest integer function).
02:09View Solutionlimx→0|x|[cosx] जहाँ [⋅] महत्तम पूर्णांक फलन है, का मान है
05:14View SolutionEvaluate : [limx→0sinxx], where [⋅] represents the greatest integer function.
06:02View SolutionEvaluate : [limx→0tanxx], where [⋅] represents the greatest integer function.
02:04View SolutionProve that [limx→0tan−1xx]=0, where [.] represents the greatest integer function.
02:46View Solution