Let f(x)=⎧⎪
⎪⎨⎪
⎪⎩x2+3x,−1≤x<0−sinx,0≤x<π/2−1−cosx,π2≤x≤π . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minima
Video Solution
Text Solution
We have f(x)=⎧⎪
⎪⎨⎪
⎪⎩x2+3x,−1≤x<0−sinx,0≤x<π/2−1−cosx,π2≤x≤π
y=x2+3x
∴ y=(x+3/2)2−9/4
∴ (y+9/4)=(x+3/2)2 which is a parabola having vertex at (−3/2,−9/4).
For y=−sinx,y=0 when x = 0 and y = -1 when x=π/2.
For y = -1 - cos x, y = -1 when x=π/2 and y = 0 when x=π.
Hence the graph of the function y = f(x) is as shown in the following figure.
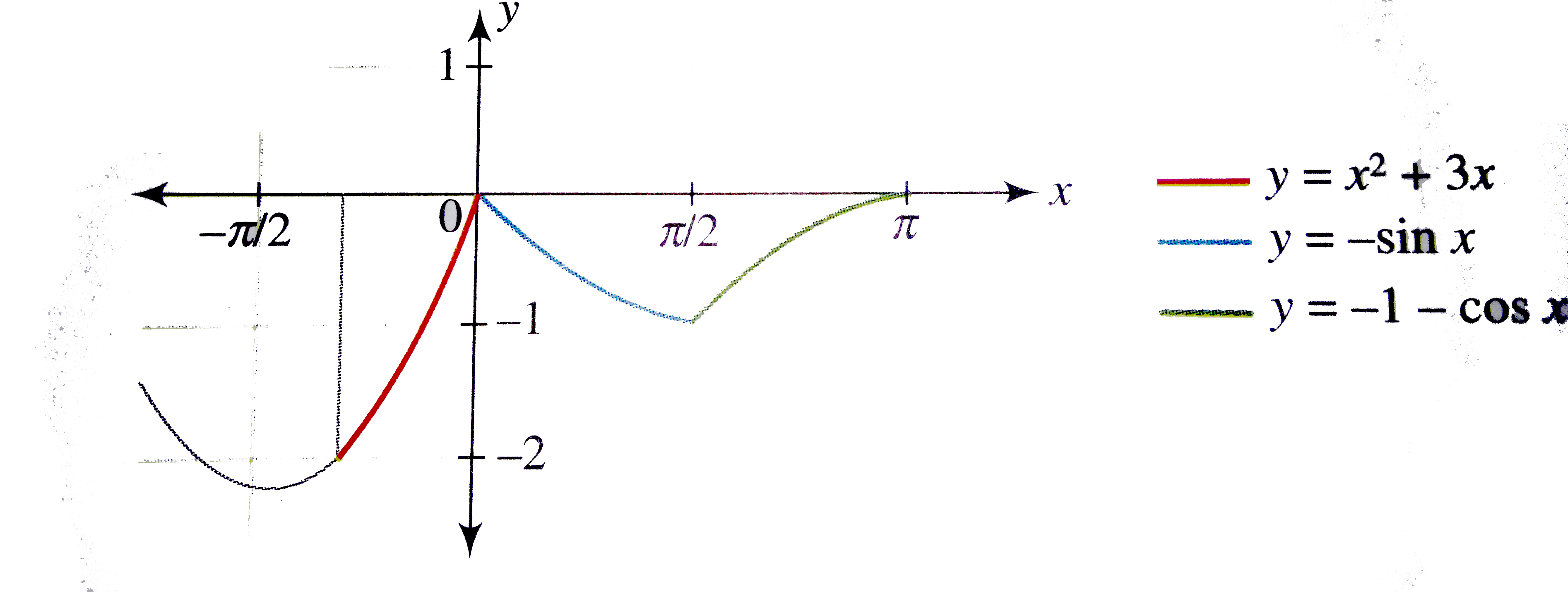
From the graph, x=π/2 is the point of local minima.
for y=−sinx,y''=sinx>0 for x∈(0,π/2). SO the curve is concave upwards.
For y=−1−cosx,y''=cosx<0 for x∈(π/2,π). So the curve is concave downwards.
Hence x=π/2 is the point of inflection.
The least value of y=f(x) occurs for y=x2+3x, when x = -1.
Hence the least value is -2. Therefore, the range is [-2, 0].
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Let f(x) = ⎧⎪⎨⎪⎩x3+x2−10x−1≤x<0sinx0≤x<x/21+cosxπ/2≤x≤x then f(x) has
View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x3+x2−10x−1≤x<0cosx0≤x<π21+sinxπ2≤x≤π Then at x=π2, f(x) has:
View SolutionIf f(x)={3x2+12x−1,−1≤x≤237−x,2<x≤3,then
View SolutionLet f(x)={1+x,0≤x≤23−x,2<x≤3
find (fof) (x).
View SolutionEvaluate : ∫30f(x)dx,
where f(x)={cos2x,0≤x≤π23,π2≤x≤3
View SolutionLet f(x)={xfor0≤x<13−xfor1≤x≤2
Then f(x) is
View SolutionIf f(x)={3x2+12x−1,−1≤x≤237−x,2<x≤3 then
View SolutionLet f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinxfor−π≤x≤−π2asinx+bfor−π2<x<π2cosxforπ2≤x≤π.
If f is continuous on [−π,π), then find the values of a and b.
View SolutionIf f(x)={x2+10≤x<1−3x+51≤x≤2
View SolutionLet f(x)={2−x,−3≤x≤0x−2,0<x<4 Then f−1 (x) is discontinous at x=
View Solution
