Solve tanx<2.Solution in Bengali
We known tan x is periodic with period π. So let us solve for x∈(−π2,π2)
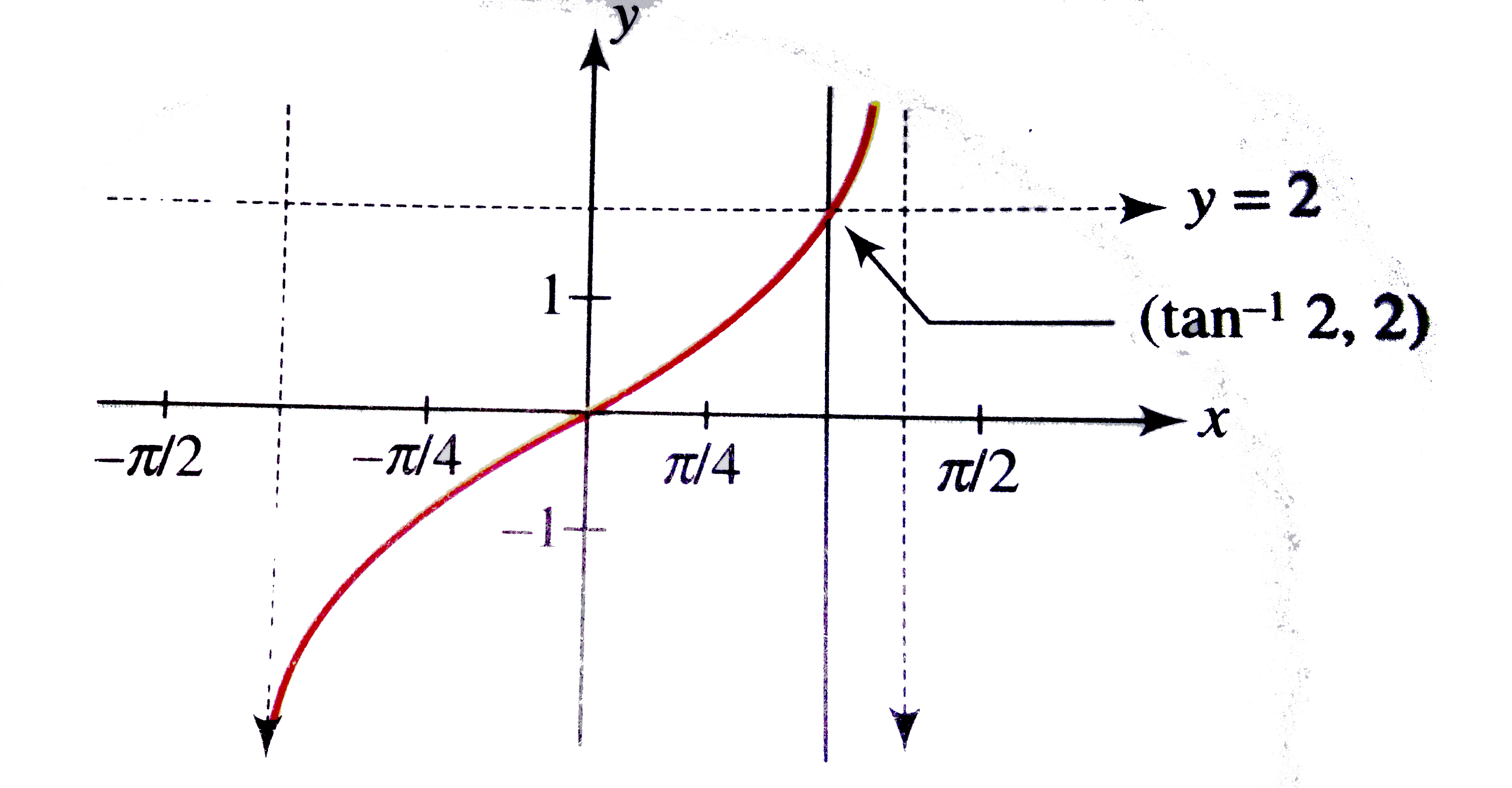
It is clear from the figure, tanx<2 when −π2<x<tan−12
General solution is nπ−π2<x<nπ+tan−12,n∈Z
⇒ x∈⋃n∈Z(nπ−π2,nπ+tan−12)
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionSolve the inequality: tan x lt 2
View SolutionSolve tanθtan4θ=1 for −<θ<π.
View SolutionSolve tanx<2.
View Solutionहल करें ( Solve ) |x|<2
View Solutionनिम्नलिखित समीकरणों को हल कीजिए -
tan−1.x2+tan−1.x3=π4,0<x<√6.
View SolutionSolve tanx−tan2x>0and|2sinx|<1 .
View SolutionSolve : tan−1(cosx1+sinx), −π2<x<π2
View SolutionSolve :
tan−13x+tan−14x=tan−1(1x),12x2<1,x≠0
View SolutionSolve tanx<2.
View SolutionSolve tanx<2.
View SolutionIf tanx<2 then
View SolutionSolve: tan3x=cot5x,(0<x<2π).
View Solution
