Solve $tan x < 2$ .

Video Solution

Text Solution

Verified by Experts

We known tan x is periodic with period $π$ . So let us solve for $x \in (- \frac{π}{2}, \frac{π}{2})$

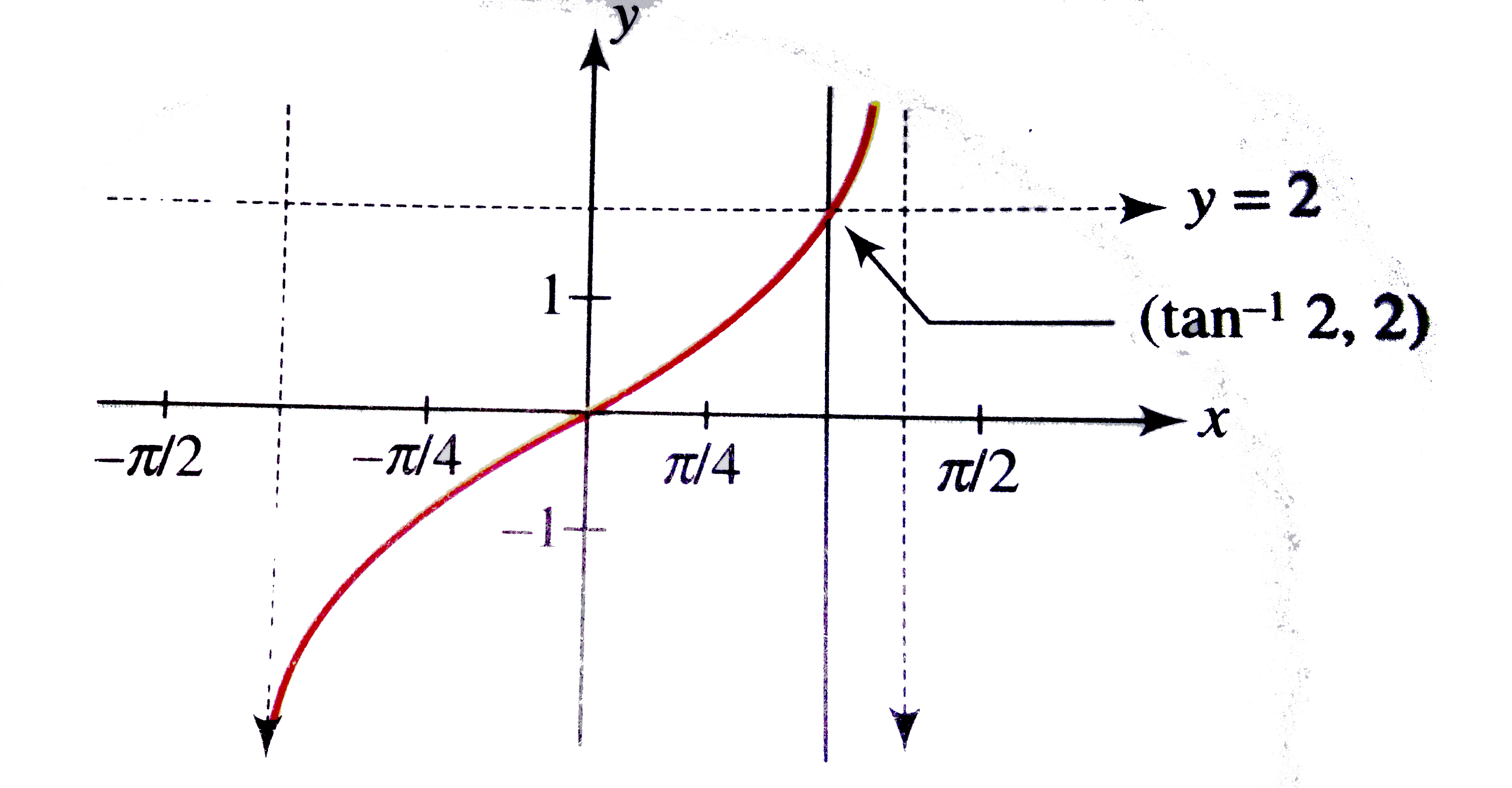
It is clear from the figure, $tan x < 2$ when $- \frac{π}{2} < x < {tan}^{- 1} 2$
General solution is $n π - \frac{π}{2} < x < n π + {tan}^{- 1} 2, n \in Z$
$\Rightarrow$ $x \in ⋃ n \in Z (n π - \frac{π}{2}, n π + {tan}^{- 1} 2)$

Updated on:21/07/2023

|

Class 12 MATHS GRAPHS OF TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-GRAPHS OF TRIGONOMETRIC FUNCTIONS-Exercises

Home
Ask Doubt
Profile