Solve : Cosx≤−12.
Video Solution
Text Solution
cos x is periodic with period 2π.
So check the solution in [0,2π].
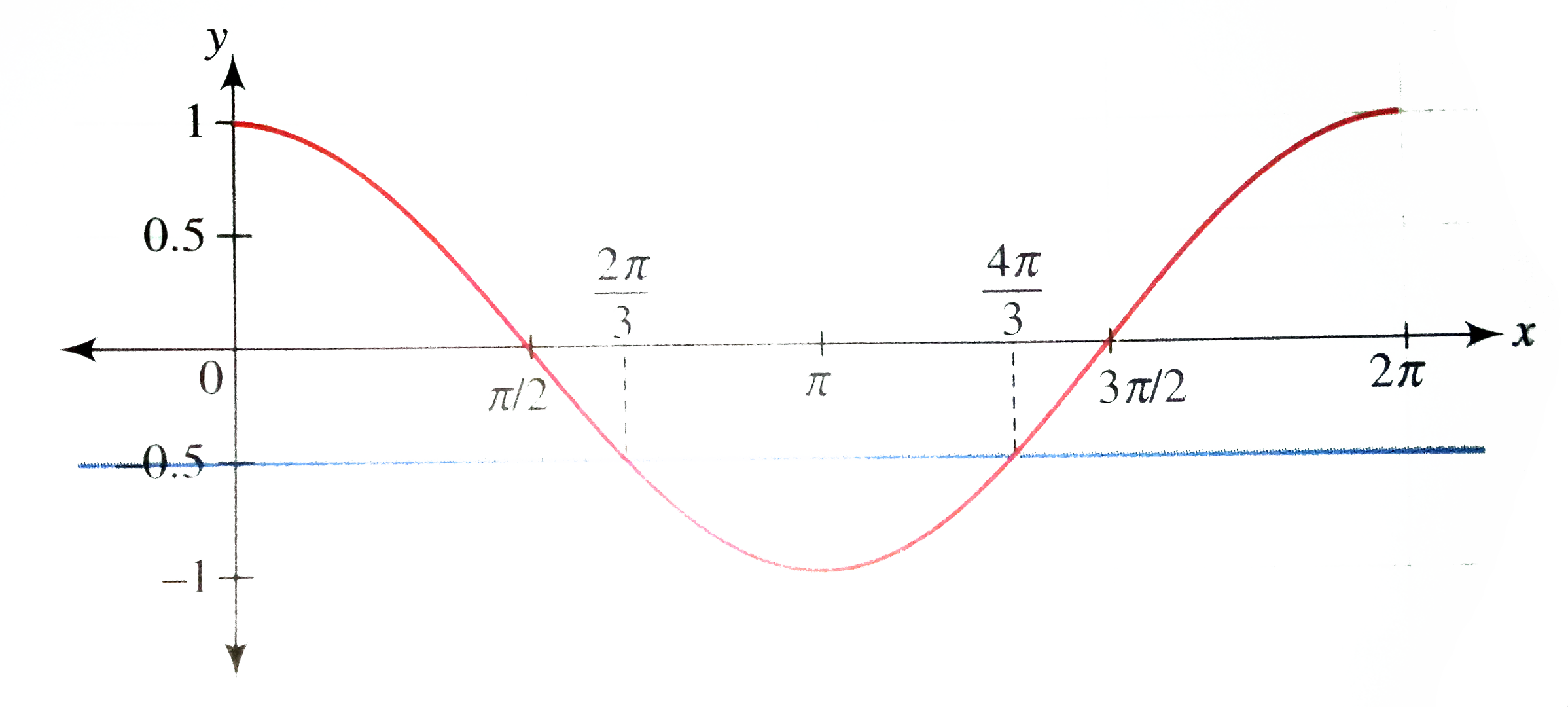
It is clear from the figure, that cosx≤−12 when 2π3≤x≤4π3.
On generalizing the above solution,
2nπ+2π3≤x≤2nπ+4π3,n∈Z
So the solution to cosx≤−12⇒x∈[2nπ+2π3,2nπ+4π3],n∈Z
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Solve : |x−3|≤1
View SolutionSolve 1≤|x−2|≤3
View SolutionSolve xx+2≤1|x|
View SolutionSolve |3x−2|≤12.
View SolutionSolve : 1x2+x≤12x2+2x+3
View SolutionSolve : −12≤4+3x5≤2
View SolutionSolve : 5x4−1≤4x−13
View SolutionSolve √x−2≤3
View SolutionSolve : 2x−1x+2≤3
View SolutionShow that 5x≤8cosx−2cos2x≤6x for x≤x≤π3
View Solution
