Let Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....Solution in Tamil
The correct Answer is:4
We have, Sk=k−1k!1−1k=1(k−1)!
Now, (k2−3k+1)Sk={(k−2)(k−1)−1}×1(k−1)!
=1(k−3)!−1(k−1)!
⇒100∑k=1!(k2−3k+1)Sk∣=1+1+2−(199!+198!)=4−1002100!
⇒1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣=4
Similar Questions
माना की Sk=1,2,……..100 उस अनंत गुणोत्तर श्रेणी का योग प्रदर्शित करता है जिसका प्रथम पद k−1k! तथा सार्व अनुपात 1k है तो 1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣का मान है
08:43View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
07:31View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣ is ____________02:32View SolutionFor k=2,3,…, let Sk denote the sum of the infinite G.P. whose first term is k2+k−2 and common ratio is 1k, then ∞Σk=1Sk2k=
View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
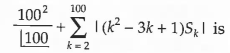is 11:19View SolutionLet Sk be the sum of an infinite G.P series whose first is k and common ratio is kk+1(k>0). Then the values of ∞∑k−1(−1)kSk is equal to
06:05View SolutionLet Sk be the sum of an infinite G.P. series whose first term is k and common ratio is kk+1(k>0). Then the value of ∞∑k=1(−1)ksk is equal to
07:37View Solution