Let be the sum of an infinite G.P. series whose first term is k and common ratio is . Then the value of is equal to Solution in Bengali
The correct Answer is:D
Step by step video, text & image solution for Let S_k be the sum of an infinite G.P. series whose first term is k and common ratio is k/(k+1) (k gt 0). Then the value of sum_(k = 1)^infty (-1)^k/s_k is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
An um contains 30 tickets numbered 1 to 30 two tickets are drawn at random the probability that both the numbers are prime is
10:55View SolutionSolve the equation 4x2+9=0 by factorisation mathod .
01:26View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
08:43View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
05:59View Solutionमाना की Sk=1,2,……..100 उस अनंत गुणोत्तर श्रेणी का योग प्रदर्शित करता है जिसका प्रथम पद k−1k! तथा सार्व अनुपात 1k है तो 1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣का मान है
06:43View SolutionLet Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
06:53View SolutionLet SK be the sum of an infinte G.P. series whose first term is K and common ratio is KK+1(K>0). Then the value of ∞∑K=1(−1)KSK is equal to
08:43View Solutionयदि एक अनंत गुणोत्तर श्रेणी जिसका प्रथम पद k और सरवणुपात kk+1(k>0) का योग प्रदर्शित करता है तब ∞∑k=1(−1)kSkका मान होगा
07:31View Solutionमाना की Sk=1,2,……..100 उस अनंत गुणोत्तर श्रेणी का योग प्रदर्शित करता है जिसका प्रथम पद k−1k! तथा सार्व अनुपात 1k है तो 1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣का मान है
02:59View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
02:32View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
11:19View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣ is ____________06:05View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
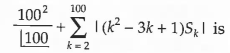is 04:34View SolutionLet Sk be the sum of an infinite G.P series whose first is k and common ratio is kk+1(k>0). Then the values of ∞∑k−1(−1)kSk is equal to
03:31View SolutionLet Sk=limn→∞n∑i=01(k+1)i. Then n∑k=1kSk equals
03:55View Solution