Let Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
Video Solution
Text Solution
The correct Answer is:4
We have, Sk=k−1k!1−1k=1(k−1)!
Now, (k2−3k+1)Sk={(k−2)(k−1)−1}×1(k−1)!
=1(k−3)!−1(k−1)!
⇒100∑k=1!(k2−3k+1)Sk∣=1+1+2−(199!+198!)=4−1002100!
⇒1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣=4
|
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - HARMONIC PROGRESSION
9 Videos
- SEQUENCES AND SERIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - RELATION BETWEEN AM,GM, HM AND SOME SPECIAL SERIES
34 Videos
- SEQUENCES AND SERIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - GEOMETRIC PROGRESSION
16 Videos
- RELATIONS AND FUNCTIONS BOOK - IIT JEE PREVIOUS YEARCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - All Questions
1 Videos
- SOLVED PAPER 2019BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -2 section-3
4 Videos
Similar Questions
Let sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
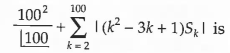 is
is
View SolutionLet Sk denote sum of infinite geometric series (K=1,2,3,.......), where first term is (k2−1) and common ratio is 1K, then the unit digit of the sum (∞∑k=1Sk2k−1), is
View Solution
Knowledge Check
Let Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k.k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
A3B2C1D0Let Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
A1−4loge√2Bloge2−1C1−loge2D1−loge4Let SK be the sum of an infinte G.P. series whose first term is K and common ratio is KK+1(K>0). Then the value of ∞∑K=1(−1)KSK is equal to
Aloge4Bloge2−1Cloge2+1D1−loge4
For k=2,3,…, let Sk denote the sum of the infinite G.P. whose first term is k2+k−2 and common ratio is 1k, then ∞Σk=1Sk2k=
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View Solutionn∑k=1(2k+3k−1)
View SolutionFind the value of 2551 S where S=50∑k=1kk4+k2+1
View SolutionFind the value of limn→∞n∑k=1k2+k−1(k+1)!.
View Solution
