If and , then find the minimum natural number n, such that
Video Solution
Text Solution
The correct Answer is:7
Obviously, it is true for all even values of n.
But for
and for ,
Hence, minium odd natural number
|
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - HARMONIC PROGRESSION
9 Videos
- SEQUENCES AND SERIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - RELATION BETWEEN AM,GM, HM AND SOME SPECIAL SERIES
34 Videos
- SEQUENCES AND SERIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - GEOMETRIC PROGRESSION
16 Videos
- RELATIONS AND FUNCTIONS BOOK - IIT JEE PREVIOUS YEARCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - All Questions
1 Videos
- SOLVED PAPER 2019BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -2 section-3
4 Videos
Similar Questions
Knowledge Check
IF an=1n+1+1 then find the value of a1+a3+a5
A1712B2712C3712D4712If 1.3+2.32+3.33+...=n3n=(2n−1)3+b4, then a and b are respectively:
An,2Bn,3Cn+1,2Dn+1,3
Let An=34−(34)2+(34)3−...+(−1)n−1(34)nandBn=1−An, then find the least value of n0,n0∈N such that Bn>An,∀n≥n0.
View SolutionComplete the following statements.
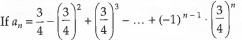 and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
View Solution13+23+33+.....+n3=n(n+1)24,n∈N
View Solution1+5+9+...+(4n−3)=n(2n−1) for all natural numbers n
View SolutionIn an AP, given an=4,d=2,Sn=−14 find n and a
View Solution∞∑n=1(14n−3−14n−1)=πn find n
View Solution
